Calcule a integral
Onde é o triângulo de vértices e
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
O problema nos pede para integrar a área de um triângulo que está em uma posição no plano cartesiano. Como é esse triângulo que devemos calcular a área?
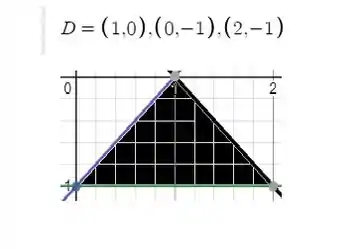
E veja que essa região da área do triângulo está abaixo do eixo do gráfico, então vamos ter uma integração bem chatinha de ser feita. Mas isso não é problema pra gente!
“Então, Mogli, como eu faço?” Como sempre fazemos: achar os intervalos de integração de cada variável e então integrar. Além disso, não podemos esquecer do problema da função que vamos integrar que não é tão amigável assim. Mas isso também não é problema pra gente!
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Como podemos definir os limites de integração? Precisamos ver como a região se comporta:
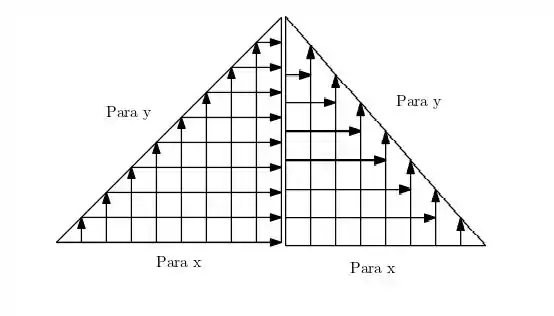
E podemos separ em partes, como foi feito na imagem. O nosso problmea então é identificar de onde as variaveis e saem e até onde elas vão.
Para a primeira parte:
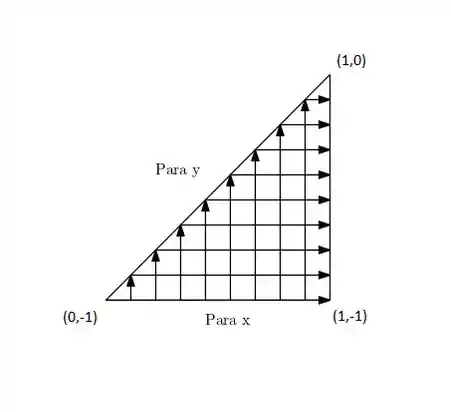
Podemos ver que parte de e percorre até bater na parede . E para ? Já é mais complicado um pouco, porque ela vai de até uma parede. Quem é essa parede? É uma reta que liga os pontos e . Assim, precisamos achar a equação dessa reta. Logo:
Esta é uma tecnica geral para acharmos a equação de uma reta que liga dois pontos. Isto é: colcoamos os dois pontos e o ponto geral e , e sempre na ultima coluna colocamos , e assim encontramos o determinante. Então para acharmos a equação da reta basta aplicarmos a regra de Sarrus. Logo:
Como saber se essa realmente é reta que liga os dois pontos basta vermos no gráfico:
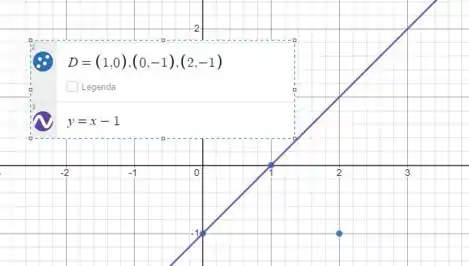
Sim, ela é reta que liga os pontos e .
Voltando ao nosso raciocinio, temos então que vai de até . Resumindo:
Já para segunda parte:
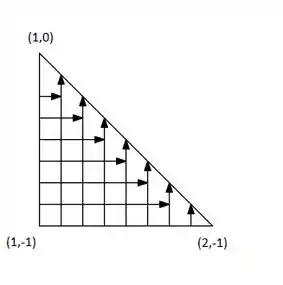
Da mesma maneira vai de e bate em uma parede. Que parede é essa? ? É uma reta que liga os pontos e . Assim, precisamos achara a equação dessa reta. Logo
Da mesma maneira que fizemos agora pouco:
Aplicando a regra de Sarrus, temos que:
Como saber se essa realmente é reta que liga os dois pontos basta vermos no gráfico:
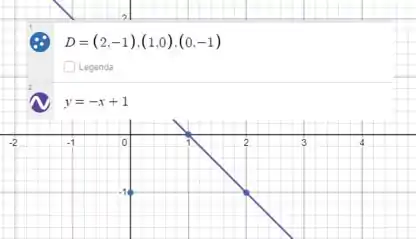
E sim, essa é a reta que liga. Agora voltando ao nosso raciocinio, vemos que vai de e bate na parede que é a reta .
E para vemos que ele vai de até .
Resumindo:
E agora achamos os noss intervalos das variaveis que temos que integrar.
Passo 3
Lembrando que tínhamos
E como fizemos em todos a nossa variável depender de , concorda que temos que fazer ou invés de ? Porque vamos terminar com uma variável no final que terá sentido algum.
Então como dividimos nossa integral em duas partes, teremos duas integrais, certo? Então:
E agora vamos ver como é essa integral?
Passo 4
E aqui uma declaração que devemos fazer: Embora tenhamos feito tudo até aqui, devemos lembrar que é uma prova que foi feita online, e, portanto, devemos realizar a prova nas mesmas circunstâncias que eles. E por que isso? Porque nesse momento chegamos em uma integral que só pode ser realizada por métodos computacionais numéricos, então vamos ver o que o computador nos dá?
Pelo desmos:
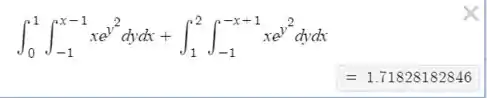
Pelo Wolfram:
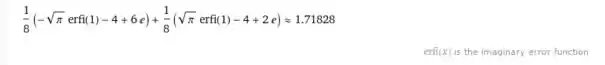
Então podemos concluir que:
Onde é o triângulo de vértices e
Resposta
Onde é o triângulo de vértices e