Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
Calcule as seguintes integrais
Passo 1
Hmm.. Que questão estranha, primeiro que ele já vem pedindo a soma de duas integrais, depois que a função dentro dela , é impossível de integrar... Isso tá me cheirando a inversão da ordem de integração, vamos fazer o esboço da região.
Na primeira integral, temos duas parábolas, mas só a parte de positivo:
Com o variando entre e , ficamos com algo assim:
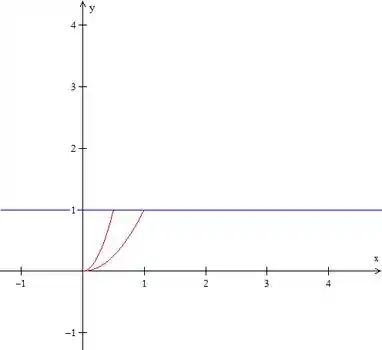
Na segunda, temos uma constante e uma das parábolas que aparece na região anterior:
Como vai de a , ficamos com isso:
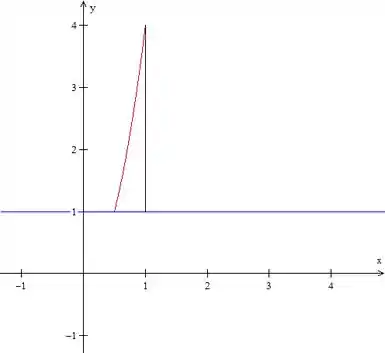
Mas é aí que a mágica acontece, porque, como a função dentro da integral é a mesma podemos desenhar as duas regiões juntas e ficarmos com:
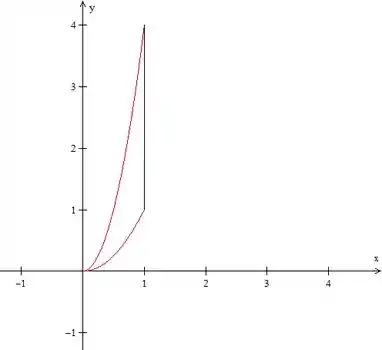
Que é uma região do tipo , então podemos sim inverter a ordem de integração, vamos ver como vai ficar!
Passo 2
Pelo desenho, dá pra ver que o vai variar entre as duas parábolar e o vai de a , então ficamos com:
Que agora sim podemos tentar resolver!
Passo 3
Vamos integrar primeiro em relação a :
Que a gente resolve pela substituição:
Então:
Aplicando os limites de integração:
Pronto, acabou nem sendo nada bizarro, viu?