2) Faça um esboço da região de integração e mude a ordem de integração na seguinte integral:
Passo 1
E aiiii... belezinha?
Nessa questão vamos esboçar a região de integração e, pra isso, vamos usar bem os limites de integração que estão nos símbolos de integral, que é (olhando de dentro pra fora),
variando de até e
variando de até .
E depois vamos mudar a ordem de integração, que é fazer algo como:
Atenção, heim!? Não é só trocar a ordem e os limites de integração. Vamos usar o esboço pra definir os novos limites de integração.
Passo 2
Já vamos começar metendo o pé na porta?
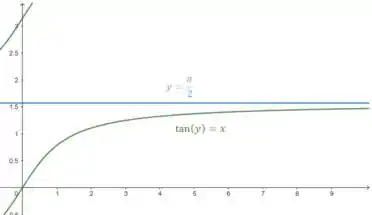
Na integral de dentro, vamos esboçar essa função feia aí, que é o que limita a parte de baixo de .
Lembra que essa tangente aí com -1 é a mesma coisa que arcotangente? É a função inversa de tangente. Se a gente representar assim:
Isso é a mesma coisa que:
Pooo... aí um pouquinho mais fazível porque a gente sabe, mais ou menos, como é o gráfico da função tangente.
Mas se não lembrar como é o gráfico, vai chutando uns valores daqueles conhecidos (0, 30, 45, 60 e 90 graus, que, em radianos fica e )

Repara que vamos começar em zero e parar láááá no infinito (rs) quando .
Esboçando só essa curva:
Passo 3
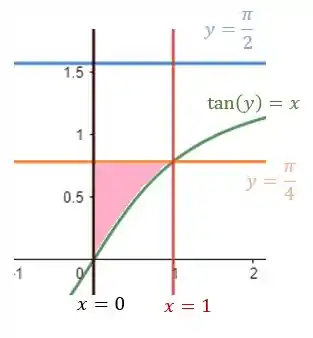
Maaas essa o é limitado, na parte de cima, por . (e temos até na tabela, né?? então essa reta vai cruzar bem bonitinho a curva em )
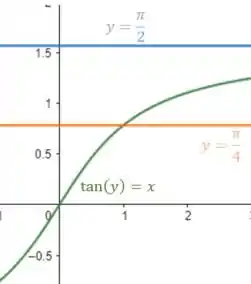
Como já estamos falando de reta. Vamos pros limites de também, que são as retas e .
Esboçando tudo e marcando a região delimitada:
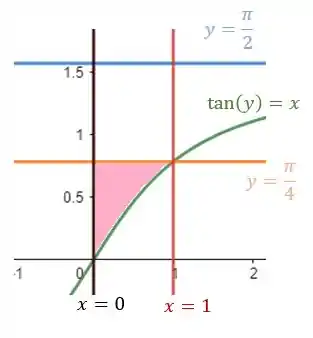
Passo 4
Pra mudar a ordem de integração... Repara que antes estávamos olhando de baixo pra cima, na integral de dentro, certo? Era o variando de até .
Agora vamos olhar da esquerda pra direita, na integral de dentro. Então vamos ter o variando de até a curva, que é .
Já para o ele varia de até .
Repara que só levamos em conta a curva feiosa uma vez, ok!?
Então a integral dupla, mudando a ordem de integração, fica:
Acabamos mais uma... Partiu pra próxima?
Resposta