Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 10
Nos exercícios 09 a 12, escreva as integrais dadas com a ordem de integração invertida
10.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema queremos inverter os limites de integração da integral
Tem alguma ideia de como fazer isso? 🤔
Na prática para passar a integral de para temos que olhar para os limites de integração de e de e tentar reescreve-las de modo que invertemos a função ou sendo os limites da última integral sempre definidos entre duas constantes.
Bora ver como é na prática? 😉
Passo 2
Nesse caso, perceba que varia entre duas constantes e . Já está definida entre duas funções e .
Esboçar as curvas no plano pode facilitar bastante o nosso trabalho, vamos fazer isso para ver o que encontramos
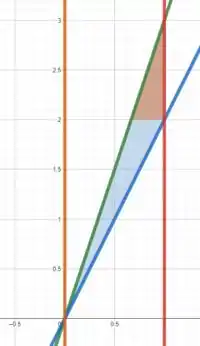
Bem mais fácil, não é?
Temos que passar a definir entre duas funções e entre duas constantes.
Horizontalmente a região de integração é limitada em duas partes distintas (azul e laranja), a primeira entre a curva azul e a reta verde e a segunda pela reta vermelha e a reta verde .
Isolando em um lado da equação, vamos obter para a primeira parte da região, temos
Já para a segunda região (laranja) é definido superiormente por uma constante e inferiormente por uma função
Então esses serão os limites de integração de .
Entendeu a ideia? 👀
Passo 3
Agora vamos analisar os limites em ,tanto na primeira como na segunda região, os limites em devem ser constantes, ou seja
Na região azul, vamos que varia de a (que é o ponto onde e se intersectam)
Já na região laranja, varia de a .
Condensando essas informações em duas integrais, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
