Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 3c.
3 - Inverta a ordem de integração das seguintes integrais duplas iteradas:
c)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
O objetivo dessa questão é conseguirmos inverter a ordem de integração para .
Pode parecer simples, só precisamos trocar as integrais de lugar e está tudo certo, não é? Infelizmente não!
Perceba que ao calcularmos essa integral dupla, no fim vamos encontrar um valor numérico. Se simplesmente invertermos as integrais, quando aplicarmos os limites de integração na última integral, vamos obter um resultado que depende de , ou seja, uma função.
Mas então como vamos fazer isso?? 🤔
Calma, vamos lá que eu te mostro.
Passo 2
Antes de tudo, vamos desenhar a região de integração.
Analisando a integral, vemos que para a região varia entre e . Já para , a região varia entre e .
Com isso, temos as seguintes equações que limitam nossa região
Plotando essas curvas, vamos obter
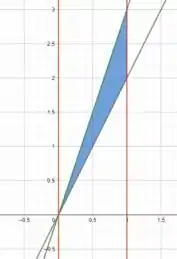
A ideia é obter o mesmo resultado a partir da mesma região descrita de forma diferente.
Antes, tínhamos variando entre duas constantes, agora é a vez de . Pelo gráfico, vemos que o maior valor de é e o menor valor é .
Podemos provar isso manipulando as equações que temos
Se o limite superior de é e de é
Se o limite inferior de é e de é
Com isso, encontramos os limites de integração para
Passo 3
Escrevendo as curvas e isolando , temos e .
Aqui temos um problema! Para a região está variando entre três curvas: , e .
Com isso, não podemos dizer que está variando entre e nem que está variando entre e .
Quando temos algo do tipo, podemos dividir a região em duas, consequentemente dividimos a integral em duas.
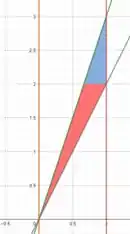
Assim, vamos descrever duas regiões.
A região azul é dada pela variação de a em e da curva e .
Como o limite superior, escrevemos como a curva maior em termo de valores, ou como a curva mais longe da origem. Os limites de integração em varia entre e , logo
Tranquilo até aqui? 👀
Passo 4
Para a região vermelha, vemos que varia entre e , já varia entre as curvas e .
Com isso, os limites de integração em vai de a e em vai de a .
Dessa forma, a integral que descreve a região vermelha é dada por
Por fim, a região de integração que tínhamos no início é a soma das regiões azul e vermelha. Logo, a integral que descreve essa região na ordem é dada pela soma das integrais
É isso! Essa resolução te ajudou? Responde Aí! ✌
