Usando a definição de integrais iteradas, calcule:

(a) O número

(b) O número

(c) Qual das seguintes relações é verdadeira: ,, ou ? Explique, usando um argumento teórico, por que já se espera que tal relação seja verdadeira, mesmo antes de se calcular e .

Letra (b)

De novo precisamos calcular a integral, vamos lá? Começando a integrar em relação a agora

Integrando em relação a

Letra (c)

Agora que sabemos o valor de e é fácil responder a primeira pergunta, não é? Os dois números são iguais!

A segunda parte da questão que é um pouco mais chata, ele pede alguma explicação teórica aqui pra explicar como poderíamos imaginar que já ia dar igual...

Analisando as duas integrais uma embaixo da outra aqui

Podemos perceber que as duas integrais tem a mesma função dentro delas!

“Ah, mas isso não quer dizer nada, isso não prova que o resultado tem que dar o mesmo.”

Se você pensou isso, ótimo! Realmente não prova nada! Para duas integrais terem o mesmo valor com certeza, elas precisam integrar a mesma função e estar na mesma região de integração.

Mas perceba o seguinte: está escrito numa região do tipo e numa região do tipo ! Então olhando assim ninguém consegue perceber que seja a mesma região, como conferimos isso?

Bom, vamos fazer um esboço da região de e inverter a ordem de integração! Se bater com os limites de provamos porque o resultado é igual =D

A região possui esses limites aqui

Portanto é limitado superiormente pela reta (vermelha) e inferiormente por (azul)

Essa segunda reta, pode ser mais simples esboçar com isso aqui

Olha o esboço então

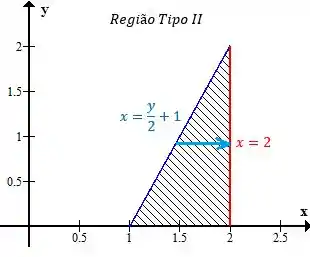
Agora vamos analisar esse mesmo esboço no tipo , pra isso precisamos escrever a reta azul como , com isso

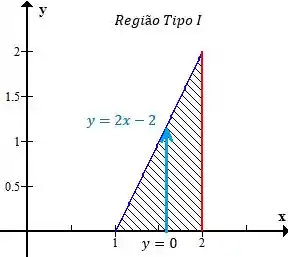
Logo os limites dessa região no tipo são

Portanto as regiões de e são as mesmas! Provando porque o resultado da integral deu igual =D