Calcule
Esboce a região de integração.
Passo 1
Vamos começar desenhando essa região de integração. Temos:
Ou seja, está entre as retas e e:
Portanto, temos essa região aqui:
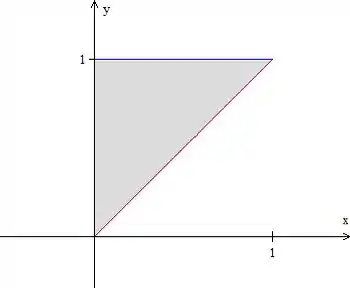
Passo 2
Agora vamos à integral
Meio difícil de integrar isso aí direto, né? Vamos tentar simplificar as coisas invertendo a ordem de integração, escrevendo a região de outra forma. A região está escrita como do tipo , vamos reescrevê-la como tipo , temos:
Aplicando isso na integral, temos
Passo 3
Agora podemos integrar isso aí em relação a :
Passo 4
Bem melhor, né? Temos um cara estranho dentro da integral, então vamos fazer:
Que assim a parada fica mais fácil de ver, agora temos que mudar os limites de integração
Agora vamos as derivadas de
Aplicando isso na integral, temos: