Calcule a integral mudando a ordem de integração
Passo 1
Bom, aqui o exercício falou pra gente mudar a ordem de integração direto né? Nem precisamos pensar duas vezes! Lembra como fazemos isso? Começamos desenhando um esboço da região.
Os limites de integração são
Po, tem uma função chata ali no meio né? “”, lembra o que isso quer dizer? Em outras palavras, isso é
O esboço dessa função no intervalo de é esse aqui
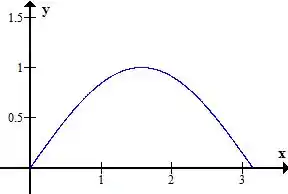
De acordo com os limites de integração, é limitado inferiormente por essa função e superiormente por , portanto o esboço da região é esse aqui
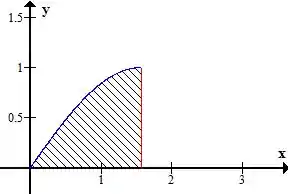
Passo 2
A nossa região inicialmente estava escrita no tipo certo? Já que estava em função de . Fazendo o contrário agora, vemos que é limitado em baixo pelo eixo , ou seja, por .
Além disso, é limitado superiormente pela função azul, que é . Ou seja
Pronto, agora é só ver os limites numéricos de . Perceba que ele também começa em , só que termina na reta vermelha, se você lembra lá do enunciado, essa é a reta , logo
Portanto a integral que precisamos calcular é
Passo 3
Bom, vamos começar integrando em então
Viu que tudo dentro da integral está em função de , certo? Então a integral fica
Passo 4
Para a integral acima ficar mais de boas pra calcular vamos utilizar o método de substituição simples na nossa integral:
Selecionamos o :
Derivando temos:
Agora temos um problema... não aparece a expressão na nossa integral! O que faremos?!
Se liga nessa identidade trigonométrica:
Isso te lembra alguma coisa?! Podemos fazer:
Os novos limites são:
Portanto, voltando pra integral:
Integrando isso aí fica