1) Considere as regiões do plano
e
Considere as integrais duplas
e
Seja .
- Escreva na forma de uma soma de integrais iteradas, integrando primeiro com respeito a e em seguida com respeito a . Efetue a integração e escreva na forma de uma integral simples
- Calcule .
- Escreva a integral , invertendo a ordem de integração: integrando primeiro com respeito a e em seguida com respeito a .
explicitando , e .
Neste item não é necessário encontra o valor numérico de , apenas escrevê-la no formato pedido.
Passo 1
Caraca! Esse problema não vai ser pequeno, então é melhor arregaçarmos as mangas e mãos as obras. Ahh! E vamos com cuidado para não nos perdermos, ok?
Bem, queremos escrever o como uma soma de integrais iteradas na forma de ...
Para fazermos isso, precisamos de duas coisas:
1º - Primeiro saber quem é a região e .
2º - Descrever cada uma dessas regiões do tipo (para dar ).
Então bora? :D
Passo 2
Bem, a região é:
Ou seja, ela tem como retas delimitantes: e . Como varia de a , nossa região é...
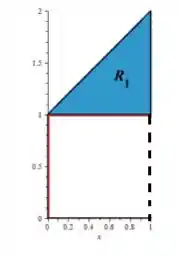
Já a descrevendo como do Tipo ... Ou seja, o continua variando em um intervalo numérico e entre funções:
Passo 3
Vamos fazer aqui a mesma coisa para a região ...
Repare que nesse caso o varia de a e o também, formando um retângulo de integração...
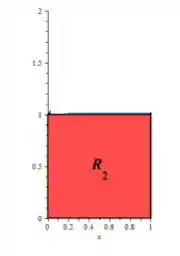
Como todo retângulo de integração, ele já está descrito como uma região do tipo e do tipo ao mesmo tempo hehe:
Passo 4
Então, o que é a soma dos dois em ...
A integral iterada já está escrita como pediu, agora é só resolver as integrais de dentro em e depois tentar unir as duas integrais em para encontrar o formato pedido. Veja só!
Passo 5
Primeiro vamos resolver a primeira integral em relação à ...
Tirando aquela função de dali de dentro...
Fazendo uma mudança do tipo
Não esqueça dos limites de integração heim!
Passo 6
Resolvendo agora a segunda integral
Passo 7
Pow, unindo o resultado dessas duas integrais já que ...
Como a função é contínua e o intervalo é o mesmo, podemos colocar essas duas integrais juntas...
Dando só mais uma simplificação...
Então para resposta do primeiro item ficar completa, nos faltava encontrar esses termos aqui:
Então, por comparação...
e
Passo 8
Aqui é apenas calcular aquela integral que definimos ali em cima...
Realizando uma mudança...
Trocando também os limites de integração...
Realizando agora uma integração por partes onde o será a função que conseguimos derivar...
Então o será apenas...
Pela fórmula de integração por partes...
Como o que queremos é a integral definida...
Passo 9
Nesse item, o que temos que fazer é escrever essa integral na ordem
Ou seja, descrever a região do tipo ...
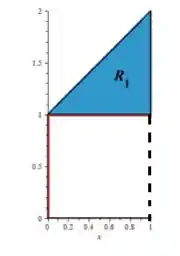
Portanto temos que o deve variar em um intervalo numérico, ou seja, de até o topo que é dado pelo encontro da reta com ...
Enquanto o tem que variar entre funções... No caso ele começa a variar na reta...
E termina de variar em ....