Considere a seguinte integral dupla
- Reescreva a integral com a ordem de integração invertida, sendo .
Passo 1
É muito importante esboçar essa região, para podermos visualizar melhor o problema. Vamos começar analisando o intervalo de , repare que o limite superior é . Se elevarmos os dois lados ao quadrado, passamos a ter:
Essa é a equação de uma circunferência de raio . Como a raiz tem que ser positiva, vamos desenhar apenas a parte com .
A outra equação que limita é (ou ), que nada mais é do que uma reta de coeficiente angular igual a – ou seja uma reta com ângulo de inclinação igual a – que desenhamos abaixo em azul.
Agora vamos analisar os limites de : temos e , ou seja, dois números. Mas não é um valor qualquer de , é exatamente o ponto em que a reta corta a circunferência, pois:
Assim, o ponto satisfaz as duas equações.
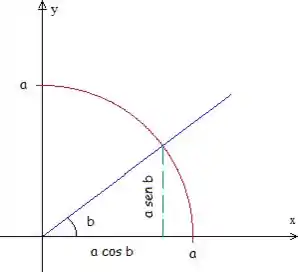
A região de integração é limitada pela reta na esquerda e pela circunferência na direita.
Passo 2
Para reescrever a região acima como tipo I, precisaremos dividi-la em duas, pois a região à esquerda de , é limitada superiormente pela reta azul, mas a direita é limitada pela curva em vermelho. Como não temos uma continuidade, vamos chamar a parte da esquerda de e a da direita de .
Para
O intervalo em dessa região vai de até , onde , portanto, temos . Em , temos embaixo e a reta azul em cima. Assim, esse domínio será da seguinte forma:
Perceba que escrevemos a equação da reta em função de .
Para
Os limites de dessa região são e , o que significa: . Em , temos novamente embaixo, mas agora, a parte de cima é limitada pela circunferência, então vamos escrever sua equação em função de .
(Apenas a parte com nos interessa)
Podemos, então, escrever esse domínio como:
Passo 3
Finalmente, podemos reescrever a nossa integral: