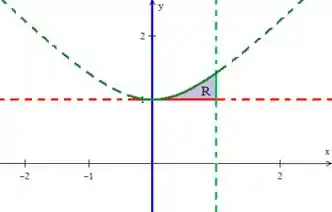
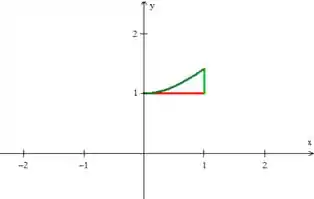
Questão 1: Considere as regiões do plano
Seja . Seja .
- Esboce hachurando. Esboce a fronteira de .
- Escreva a integral dupla
- Escreva a integral dupla
- Seja
- Calcule .
Na forma de uma integral iterada integrando primeiro com respeito a e em seguida com respeito a .
Na forma de uma integral iterada integrando primeiro com respeito a e em seguida com respeito a .
Efetue a integração e escreva na forma de uma integral simples
Explicitando, e .
Obs.: Neste item não é necessário encontrar o valor numérico de , apenas escrevê-la no formato pedido.
Passo 1
Ok! Não há tempo a perder nessa prova, pois ela é um pouco grandinha, então vamos nessa?
O primeiro item nos pede que desenhemos a região . Como sabemos, ele é a intersecção de três regiões:
Veja que com essas três regiões, tiramos algumas igualdades muito interessantes pra gente:
Então, basicamente o que temos que fazer aqui é desenhar o gráfico no de todas essas igualdades. Vamos começar com as três últimas que é um pouco mais fácil, afinal todas elas nos representam retas...
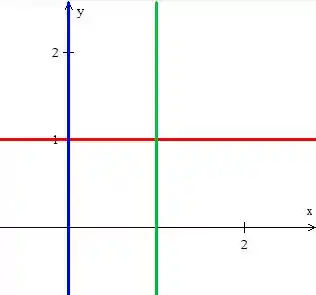
Para a primeira curva, precisamos pensar um pouco mais, pois ela não tão “trivial” assim. Mas veja que elevando em ambos os lados ao quadrado e jogando pro outro lado...
Veja que essa curva já é conhecida! Ela é uma hipérbole no plano ...
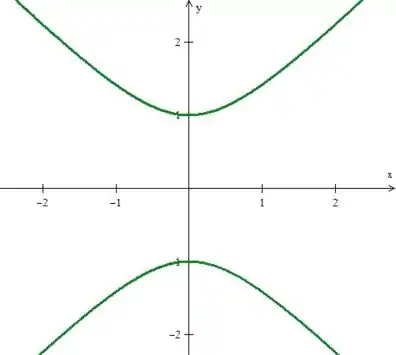
Veja então que a nossa região é a intercessão te todas essas curvas... Como queremos a parte onde , a região está representada como sendo...
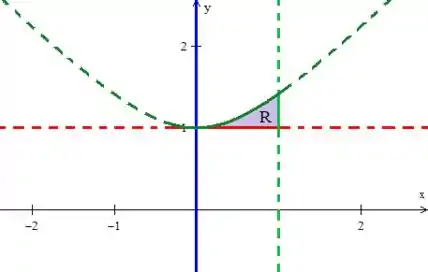
A fronteira de então é:
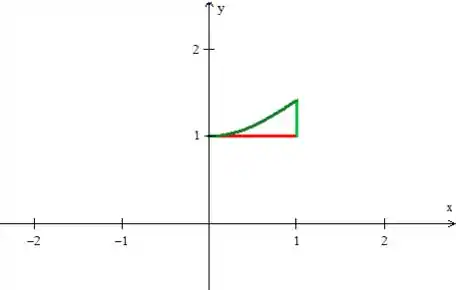
Passo 2
Agora vamos escrever a integral dupla abaixo com relação a , na mais interior, e depois, na mais externa, em relação à nessa ordem:
Sempre em integrais duplas, a variável que está variando por último deve variar entre intervalos numéricos reais. Como é a variável mais externa, então ela vai assumir esse papel. Isso significa que devemos escrever a região como do TIPO I:
Veja que nesse caso, varia de até ...
Enquanto varia da reta até o “teto” que é a hipérbole...
Então...
Passo 3
Agora vamos fazer o mesmo que fizemos no item anterior, mas dessa vez, vamos escrever na ordem...
Onde agora quem vai variar entre intervalos numéricos. Ou seja, vamos descrever agora como sendo uma região TIPO II:
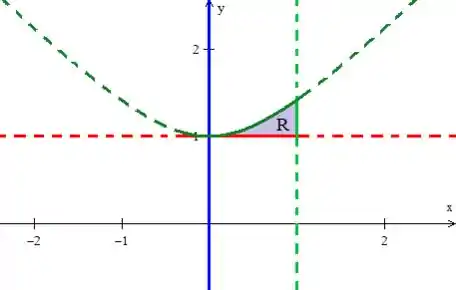
Mas veja que para isso, precisamos encontrar qual é o ( máximo) de variação da região, já que o mínimo é dado pela base reta onde ...
No desenho da nossa região, conseguimos identificar que o valor máximo que assume é dado pelo ponto mais de cima definido pelo encontro da reta verde claro com a hipérbole em verde escuro. Esse ponto é facilmente encontrado pegando a reta e substituindo na equação da hipérbole...
Logo...
Ok! Mas ainda falta a variação de e, ora... Se ficou com o papel de , o deve ficar com o papel de e variar entre curvas, ou seja, deve variar entre duas paredes agora...
A parede direita é a hipérbole...
Enquanto a parede a esquerda é a reta ...
Então...
Passo 4
O que vamos fazer agora é escrever essa integral aqui
Para
Essa integral dupla aí em , pode ser facilmente descrita na sua forma iterada, já que...
Então...
Perceba que podemos pegar qualquer uma das duas integrais iteradas que encontramos para , mas é mais aconselhável à primeira:
Porque assim teremos duas integrais escritas nas mesmas ordens, enquanto os limites mais externos sendo os mesmos, o que facilita o nosso trabalho !
Passo 5
Podemos então agora calcular a integral de dentro de ambas! Vamos começar com a primeira...
Fazendo uma substituição simples...
Não se esqueça de trocar os limites também...
Passo 6
Vamos então calcular agora a integral de dentro, mas da segunda integral dupla daquele ...
Passo 7
Então...
Onde, por comparação, temos...
, e
Passo 8
Finalmente, vamos encontrar o valor final de ...
Fazendo uma substituição simples...
E...
Bem, essa integral aí se resolve fazendo uma integração por partes, onde a gente deriva e o que o multiplica a gente integra:
Logo...
Resposta