A região do plano é dado por . Se for uma função contínua sobre então a integral dupla é igual a
Passo 1
Bem, infelizmente não tem nenhuma resposta com
Pois se não seria essa na cara. O fato de não ter essa resposta significa que o problema quer que troquemos a ordem das variáveis de integração.
Passo 2
Para fazer isso, primeiro devemos trocar a ordem da configuração da descrição da região. Desenhando essa região no plano colocando essas curvas no :
Repare que a região é...
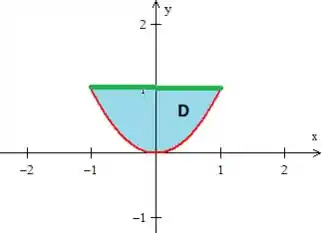
Com variando entre números, ela está configurada como região de tipo . Então mudemos isso!
Passo 3
Para classificar a região como do tipo , coloquemos o variar entre números...
Enquanto o , varia de um ramo da parábola ao outro...
Montando a integral com essa variação...