Seja a regição do plano limitado pelas curvas ee uma função contínua arbitrária em . Então,
é igual a qual mudança de ordem
Passo 1
Pra fazer essa mudança de ordem vamos precisar primeiro entender direitinho a região em que estamos trabalhando. Pra isso é importante conhecers os pontos ondes as funções se cruzam.
Bom, então se a gente fosse esboçar seria algo assim:
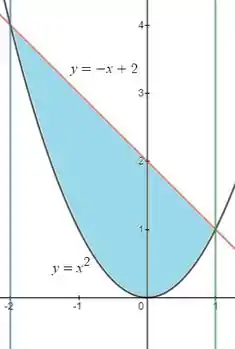
Observa que os pontos onde a função se cruza são o -2 e o 1. Agora, para escrever como uma função do tipo 2, vamos precisar fazer uma pequena divisão nessa função. Vamos ficar com algo mais ou menos assim.
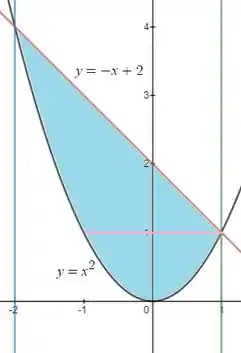
Se você for observar, adicionei uma reta y=1, pois, uma vez que o y vai variar entres constantes, vamos precisar dessa divisão.
Passo 2
Acompanha comigo, agora, se você for observar, vou ter que dividir em duas integrais diferentes, a primeira (região AZUL) e a segunda (região VERDE).
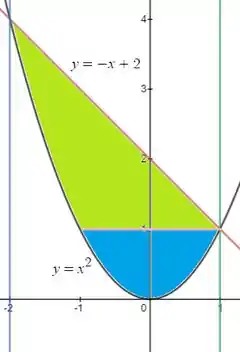
A azul vamos escrever com variando entre 0 e 1. Enquanto pra ver o intervalo de variação do x, vamos precisar isolar o mesmo. Observa que ele vai variar entre o lado esquerdo da parábola, e o lado direito.
Isso significa que x vai varia entre e .
Então a integral que vai representar a região Azul ficará como:
Passo 3
Pra concluir vamos precisar ainda escrever a região verde. Bom, ela vai ser no mesmo esquema da azul. Observa que o y agora varia entra o y=1 e o ponto mais alto que seria o y=4. Enquanto isso o x varia entre o lado esquerdo da parábula, e a reta. Pra isso, vamos isolar o x. (observe que o lado esquerdo da parábula já determinamos como .
Bom, com isso a gente já consegue escrever a integral que representa o lado verde.
Passo 4
Agora é só juntar as duas integrais. Ficamos então com