- Troque a ordem de integração em:
Passo 1
Pois bem! Em problemas como esse, troca de ordem de integração, devemos sempre começar fazendo um esboço da região.
Para fazermos isso, você terá que retirar da integral, duas informações maravilhosas que são o intervalo de (que no caso é o intervalo de fora):
e o intervalo de :
OBS. IMPORTANTE: Pow! Repare que com o variando em um intervalo numérico bem definido e o entre funções nos configura uma região do tipo I e o que devemos fazer é basicamente transforma-la em uma região do tipo II. !
Passo 2
Com essas duas informações de desigualdades conseguimos definir equações importantes:
Agora estamos preparados para desenhar a região e a boa notícia é que para fazer isso, basta colocar essas quatro equações em forma de curvas no plano , Veja:
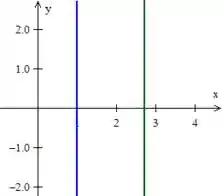
- A primeira equação, , nos representa uma reta paralela ao eixo e que passa justamente por . (Reta azul)
- A segunda é parecida com essa primeira, mas passa por (mais ou menos igual ). (Reta verde)
- Quanto à terceira curva, , ela nos representa o próprio eixo . :D (Reta amarela)
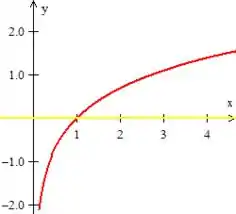
- A quarta, não se preocupe, é apenas o gráfico da função logarítmica; Veja! (Curva vermelha)
Juntando as curvas em um único gráfico (você já pode ir desenhando elas no mesmo gráfico) conseguiremos entre elas a região que estamos trabalhando entre elas :D
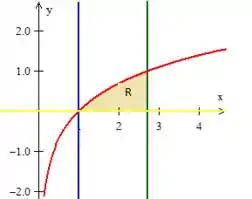
Região encontrada... Basta que troquemos e a descrevemos do outro tipo como havíamos comentado: Região do Tipo II. Então venha comigo! :D
Passo 3
Nessa configuração de Região, devemos pegar o variando em um intervalo numérico.
Mas espera um minuto! Ele está variando de até a onde?
Bem, repare então que precisamos definir qual é aquele ponto de intersecção entre a reta verde e a curva vermelha:
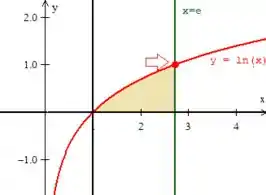
Fazer isso é bem simples, basta substituir o no logaritmo:
Então agora podemos falar sem dúvidas que o varia de até esse ponto:
Passo 4
Enquanto isso, o precisa variar de uma curva até a outra.
Repare que conforme o aumenta, ele entra primeiro na região na função logarítmica
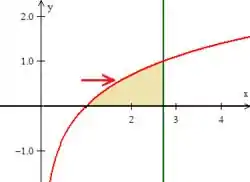
e sai na reta verde
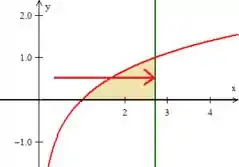
Logo
A curva vermelha tem equação , ou, isolando o , .
A reta verde é ; portanto, ganhamos:
Passo 5
Logo a região descrita do tipo II é:
Montando a integral lembrando que o limite numérico sempre vem primeiro, ganhamos: