Troque a ordem de integração em:
Passo 1
A gente só tem que inverter a ordem mesmo, nem precisa se preocupar em calcular a integral, pelo menos.
A gente tem uma região do tipo 2 e temos que passar para tipo 1, mas vamos esboçar a região pra facilitar, como a gente viu na teoria.
Primeiro temos , que basicamente é uma semicircunferência com x negativo.
E depois temos a parábola .
Lembrando que os limites de são 0 e 1, ficamos com isso:
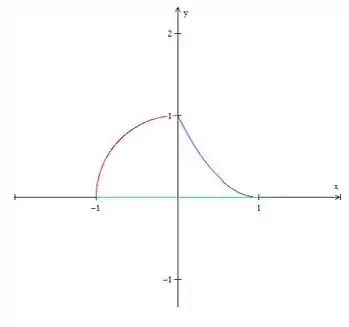
Passo 2
Bem, pelo desenho, dá pra ver que e que o limite inferior deé 0, só que o limite superior não pode ser escrito com uma equação só... Mas isso não é problema! A única cosa que vamos ter que fazer é separar a integral em duas.
Como o ponto que separa os dois gráficos é , então uma vai ser e a outra , algo desse tipo:
Então o que só falta mesmo é achar quem são esses g(x) e h(x)!
Passo 3
g(x) vai ser o gráfico que lá em cima a gente desenhou em vermelho, da circunferência:
E h(x) vai ser a parábola em azul:
Então, finalmente, vamos chegar em: