- Troque a ordem de integração em:
Passo 1
Pois bem! Em problemas como esse, troca de ordem de integração, devemos sempre começar fazendo um esboço da região.
Para fazermos isso, você terá que retirar da integral, duas informações maravilhosas que são o intervalo de (que no caso é o intervalo de fora):
e o intervalo de :
OBS. IMPORTANTE: Pow! Repare que com o variando em um intervalo numérico bem definido e o entre funções nos configura uma região do tipo II e o que devemos fazer é basicamente transforma-la em uma região do tipo I. !
Passo 2
Com essas duas informações de desigualdades conseguimos definir equações importantes:
Agora estamos preparados para desenhar a região e a boa notícia é que para fazer isso, basta colocar essas quatro equações em forma de curvas no plano , Veja:
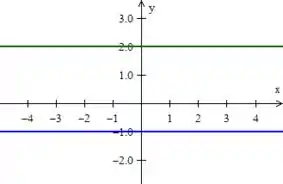
- A primeira equação, , nos representa uma reta paralela ao eixo e que passa justamente por . (Reta azul)
- A segunda, , é parecida com essa primeira, mas passa por . (Reta verde)
- Quanta a essa terceira equação, , bem ela nos representa uma parábola, mas atenção! Pois essa parábola não está ao redor de como estamos acostumados e sim ao redor de :
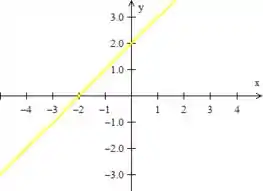
- A última igualdade, , nos representa uma reta. Caso passamos esse pro outro lado, , e desenhamos essa reta, teremos:
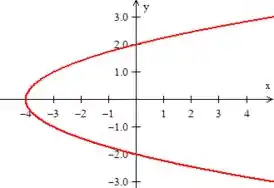
Repare que ela tem a boca pra direita afinal o é positivo além disso ela passa por .
Juntando as curvas em um único gráfico (você já pode ir desenhando elas no mesmo gráfico) conseguiremos entre elas a região que estamos trabalhando entre elas :D
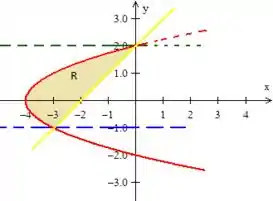
Região encontrada... Basta que troquemos e a descrevemos do outro tipo como havíamos comentado: Região do Tipo I. Então venha comigo! :D
Passo 3
Bem...! Eu quero que você note que para fazer uma descrição dessa região como do tipo , devemos ter o variando entre duas únicas curvas distintas. O problema é que isso não acontece aqui:
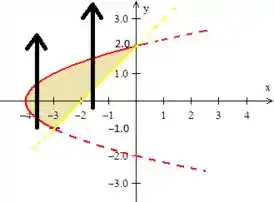
Por um lado o varia de um pedaço da curva vermelha até o outro pedaço dessa mesma curva (deslize o seu dedo na primeira reta preta); e por outro lado ele varia da reta amarela até a curva vermelha (deslize o seu dedo na segunda reta preta).
Como isso não pode acontecer para descrevermos essa região em uma região do tipo devemos desmembrar essa região em duas partes:
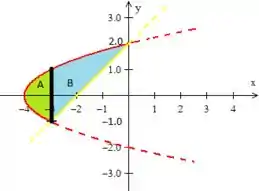
Então descrever a Região no tipo é descrever essas duas regiões separadamente e depois somar tudo. Apenas me acompanhe! :D
Passo 4
Vamos descrever aqui a Região .
Na região do tipo , o deve variar em um intervalo numérico bem definido. Aparentemente ele varia de até , mas na matemática precisamos de certeza!
Como estamos dividindo as regiões exatamente em cima do ponto de encontro entre a reta amarela e a curva vermelha, basta que encontremos esse ponto resolvendo o sistema com a equação da amarela e da vermelha:
Igualando...
onde resolvendo a equação...
com isso, substituindo na primeira equação, obtemos...
Descartamos a segunda opção por enquanto, pois onde concluímos que de fato
Passo 5
Quanto ao na região varia de um pedaço da vermelha até o outro.
se isolarmos na equação da curva vermelha (parábola) o , vamos obter:
Logo:
Passo 6
Repetindo o processo, mas agora para a parte da região, devemos encontrar a variação de .
Como encontramos que a intercessão da reta amarela com a parábola foi
só podemos ter
Veja:
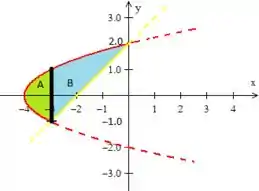
Enquanto ao em ...
Passo 7
Portanto, concluímos que a parte :
Gerando a integral dupla... (lembre-se que o limite numérico sempre vem primeiro)
E a parte ...
Gerando
Concluindo que a Região é a soma das duas partes