Troque a ordem de integração para calcular
Passo 1
A região está escrita como tipo II, temos e . Antes de trocar essa ordem de integração, vamos fazer um esboço desse domínio.
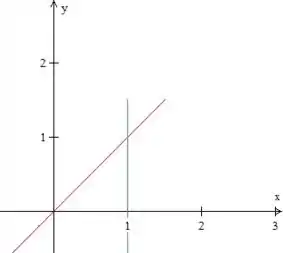
Passo 2
Para escrever a região como tipo I, teremos variando entre números. Pelo próprio gráfico, vemos que:
Pela figura, vemos também, que o limite inferior de é (o eixo ), falta então, descobrir o superior. Para isso, basta escrever a equação da reta vermelha em função de , o que é bem simples. Em vez de termos , teremos .
Então, o domínio passa a ser
Passo 3
Vamos, agora, levar esses valores para a integral, invertendo a ordem .
Passo 4
Começaremos integrando em relação a :
Passo 5
Agora vamos integrar em relação a , fazendo a substituição .