O valor da integral
é
Passo 1
Bom, pra começar essa questão, por Fubini, observa que teríamos de integral uma vez que integraríamos primeiro em y. Você saber fazer essa integral?
Eu não sei, ahhaha.
Por essa razão a primeira coisa que temos que fazer é pensar em inverter a ordem de integração. Bora dar uma olhada na região que nós estamos trabalhando.
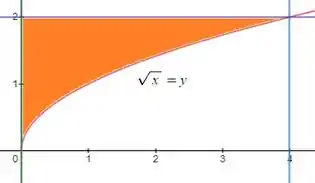
Se você for observar, estamos trabalhando em cima da região de destaquei de laranja. Nosso variando entre 0 e 4, e o variando entre e 2.
Bom, então como temos , isolando o ficamos com .
Então agora, você consegue me acompanhar pelo gráfico, ficamos com
Passo 2
Com a ordem de integração mudada, só remontar a integral e resolver! A integral que antes era
Agora pode ser reescrita como