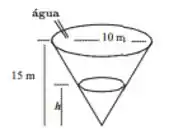
Enche-se de água um reservatório, cuja forma é de um cone circular reto (veja a figura), a uma taxa de . O vértice está a do topo e o raio do topo é de . Com que velocidade o nível da agua está subindo no instante em que ?
Passo 1
A questão pede a variação da altura da água quando a altura é . Temos a taxa de variação de seu volume, que é . Sabemos também que o volume do cone é dado por
Além disso, o enunciado diz que o raio do cone é . Assim:
e
Passo 2
Para achar a taxa de variação da altura, teremos que derivar implicitamente a equação que dá o volume em relação ao tempo.
Passo 3
Agora só precisamos substituir as informações dadas nos enunciados. A taxa de variação do volume, , é e a altura é . Então:
Resposta
Exercícios de Livros Relacionados
Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
37. No exercio 36, se o nível de água estiver decrescendo a uma taxa de 25cm/min quando a profundidade é de 3m, com que velocidade a água está sainda da tina?
39. O volume de um balão está decrescendo a uma taxa proporcional à sua área superficial. Mostre que o raio do balão diminui a uma taxa constante.
Um tanque com a forma de cone invertido está sendo esvaziado a uma taxa de 6m 3 / m i n . A altura do cone é de 24 m e o raio da base é de 12 m . Ache a velocidade com que o nível de água está baixand
30. A demanda por um determinado tipo de cereal é dada peal equação p x + 50 p = 16.00 0 onde x milhares de caixa são demandados quando o preço por caixa for p. Se o preço corrente for de $1,60 por ca