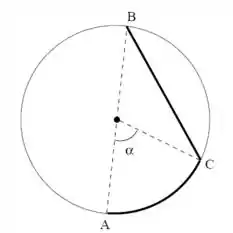
Para ir de um ponto a um ponto diametralmente oposto de uma piscina circular de de diâmetro, uma pessoa pode caminhar (com velocidade constante) pela borda da piscina até um ponto e nadar (com velocidade constante) em linha reta até o ponto (veja a figura).
Sabendo que ela pode caminhar vezes mais rápido do que pode nadar, determine, em termos de , as trajetórias que o levam ao seu destino no maior e no menor tempo.
(Obs.: Considere que ela pode somente caminhar ou somente nadar.)
Passo 1
Vamos escrever então uma fórmula para reunir toda a distância. Ele começa andando por uma fração de do perímetro da piscina, ou seja:
Para descobrir o , vamos usar um negócio que talvez você esteja enferrujado e mal lembre: Lei dos Cossenos. Rapaz, dois lados do triângulo passando pelo centro e pelos pontos e tem dimensão dada pelo raio . O ângulo de abertura ali é de . A Lei dos cossenos será essa aqui embaixo:
Sabendo então que , que e ainda que , substituímos ali:
Bom, queremos o menor tempo, certo? Então precisamos de uma função . Se no pedaço fora da piscina a velocidade vale o dobro, podemos reescrever, usando como velocidade de um valor qualquer , essa equação assim:
Passo 2
Para otimizá-la devemos derivá-la e igualá-la a zero e comparar com os valores das pontas do domínio, ou seja, e .
Vou chamar
Passo 3
Somando a esses dois pontos a outra ponta do domínio do alpha, que é dado por , temos três pontos para analisar se são máximos ou mínimos:
Considerando que é uma constante positiva, colocamos em ordem crescente os valores de tempo acima (para se guiar na ordem, use a aproximação de e ):
Em termos de , fica assim:
Ou seja, o que garante maior tempo é e o que garante o menor tempo é .