![]()
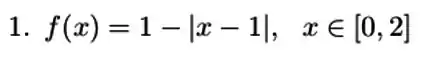
Passo 1
O Teorema de Rolle só pode ser aplicado se a função é diferenciável no intervalo tratado.
Uma função polinomial, mesmo com módulo, será sempre continua no seu intervalo de domínio. Então, resta analisar a derivada na função:
Derivando:
Pelas derivadas laterais, o ponto de mudança de domínio, , vai ter derivadas laterais diferentes e, portanto, não será diferenciável:
A função não é diferenciável em .
Portanto, nada de Teorema de Rolle nesse intervalo.
Resposta
![]()