![]()
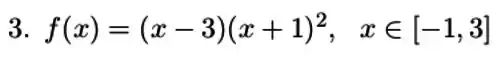
Passo 1
Para ver se a função satisfaz as hipóteses do teorema de Rolle temos que garantir que:
- A função seja contínua para todo o intervalo fechado .
- A função seja derivável para todo o intervalo aberto .
Passo 2
A função é uma função polinomial, que é contínua para todo . Assim, garantimos a primeira condição.
Passo 3
Como se trata de uma função polinomial, já sabemos que ela é diferenciável em todo o seu domínio. E nesse caso, o dominio dela é todo o .
Assim, ela também é diferenciável no intervalo aberto .
Então, o Teorema de Rolle se aplica a essa função.
Resposta
![]()