Enuncie corretamente o Teorema do Valor Médio e descreva graficamente o seu significado geométrico.
Passo 1
Bem, essa pergunta é totalmente teórica, aí não tem jeito, tem que saber mesmo. A definição do TVM é:
Se uma função é contínua no intervalo fechado e derivável no intervalo aberto , então existe um número tal que:
Passo 2
-
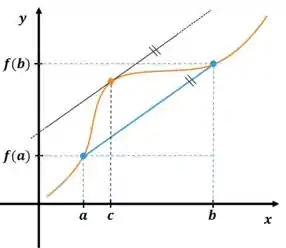
A interpretação geométrica é que a reta tangente ao gráfico de no ponto é paralela à reta que passa pelos pontos e :
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejaf x = tg x . Mostre que f 0 = f ( π ) , mas não existe um número c em ( 0 ,π ) tal que f ' c = 0 . Por que isso não contradiz o Teorema de Rolle?
Suponha que f seja uma função ímpar e derivável em toda a parte. Demonstre que para todo o número positivo b existe um número c em ( - b , b ) tal que f ' c = f b b .
Demonstre a identidade arcsen x - 1 x + 1 = 2 arctg x - π 2
Mostre que a equação 2 x - 1 - s e nx= 0 tem exatamente uma raiz real.
Dois corredores iniciam uma corrida no mesmo instante e terminam empatados. Demonstre que em algum momento durante a corrida, eles tinham a mesma velocidade. [Sugestão: Considere f t = g t - h ( t ) ,