8. Uma partícula se desloca ao longo da parábola no primeiro quadrante de modo que sua coordenada (medida em metro) aumente a uma velocidade constante de . Qual é a derivada em relação ao tempo do ângulo de inclinação da reta que liga a partícula à origem quando .
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos um probleminha de taxa relacionada!
Nós temos um ponto que se mexe ao longo da parábola a uma velocidade de (na coordenada ). Agora vamos escolher um ponto qualquer dessa parábola e liga-lo até a origem, formando assim um trigângulo.
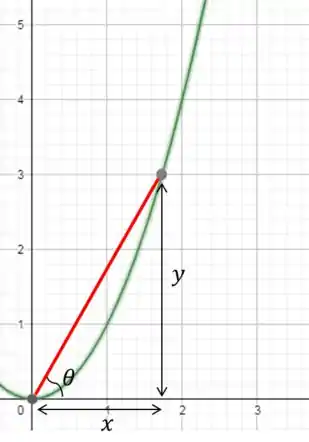
Repara que desenhando o que problema descreve temos uma triangulo retângulo. Então vamos usar essa informação para fazer as correlações.
Bora lá!
Passo 2
A gente começa estabelecendo uma relação entre os lados do triângulo. Como temos um triângulo retângulo, vamos usar o Teorema de Pitagoras.
Mas repara que essa relação não nos dá um ângulo, por isso vamos usar a definicação de tangente.
Onde é altura e é a distância horizontal.
Mas ainda temos a variável e só queremos trabalhar com e . Então temos que lembrar que e substituir.
Agora podemos relacionar a taxa de variação de com a de . Então vamos derivar essa função!
Passo 3
Agora vamos derivar implicitamente em relação a e ,
Derivando,
Lembrando que a derivada de tangente é secante ao quadrado.
Como queremos a variação do ângulo, vamos isolar
Mas lembra que,
Logo,
Agora vamos substituir com os dados fornecidos pelo enunciado!
Passo 4
O enunciado diz que a coordenada aumenta a uma velocidade constante de . Ou seja,
Agora precisamos achar quem é . Para isso, temos que lembrar que ele quer a variação quando . Com essas informações, podemos montar o seguinte triângulo retângulo para achar :
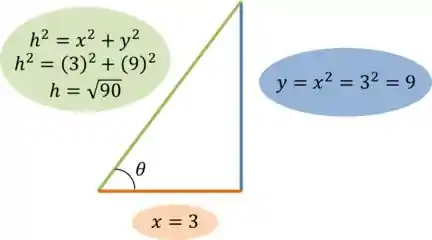
Calculando ,
Agora podemos substituir tudo na nossa expressão de .
Passo 5
Tinhamos que
Substituindo os valores encontrados,
Prontinho!