Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Frações Parciais

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

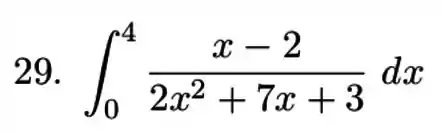
Passo 1

Vamos começar vendo se teria como simplificar esse denominador

2 x 2 + 7 x + 3

2 x 2 + 7 x + 3 = ( x + 3 ) ( 2 x + 1 )

Então nossa integral ficaria

∫ x - 2 2 x 2 + 7 x + 3 d x = ∫ x - 2 x + 3 2 x + 1 d x

Passo 2

Isso ficou com cara de frações parciais né? Vamos aplicar

x - 2 x + 3 2 x + 1 = A x + 3 + B 2 x + 1

Colocando tudo sob o mesmo denominador

x - 2 x + 3 2 x + 1 = A ( 2 x + 1 ) ( x + 3 ) ( 2 x + 1 ) + B ( x + 3 ) ( x + 3 ) ( 2 x + 1 )

x - 2 = 2 A x + A + B x + 3 B

x - 2 = x 2 A + B + A + 3 B

Dái, sabemos que

2 A + B = 1

A + 3 B = - 2

Resolvendo o sisteminha, ficamos com

A = 1

B = - 1

Então

x - 2 x + 3 2 x + 1 = 1 x + 3 - 1 2 x + 1

Aplicando na nossa integral ficamos com

∫ x - 2 2 x 2 + 7 x + 3 d x = ∫ 1 x + 3 d x - ∫ 1 2 x + 1 d x

Passo 3

Agora só falta resolver as integrais

∫ 1 x + 3 d x

Podemos utilizar a substituição

u = x + 3

d u = d x

∫ 1 x + 3 d x = ∫ d u u = ln ⁡ u

Desfazendo a substituição ficamos com

∫ 1 x + 3 d x = ln ⁡ ( x + 3 )

Fazendo bem semelhante para

∫ 1 2 x + 1 d x

Ficamos com

∫ 1 2 x + 1 d x = 1 2 ln ⁡ 2 x + 1

Passo 4

Por fim, aplicando na nossa expressão ficamos com

∫ x - 2 2 x 2 + 7 x + 3 d x = ∫ 1 x + 3 d x - ∫ 1 2 x + 1 d x

∫ x - 2 2 x 2 + 7 x + 3 d x = ln ⁡ x + 3 - 1 2 ln ⁡ 2 x + 1

E aplicando os limites de integração

∫ 0 4 x - 2 2 x 2 + 7 x + 3 d x = ln ⁡ 4 + 3 - 1 2 ln ⁡ 8 + 1 - ln ⁡ 0 + 3 + 1 2 ln ⁡ ( 0 + 1 )

∫ 0 4 x - 2 2 x 2 + 7 x + 3 d x = ln ⁡ 7 - ln ⁡ 9 - ln ⁡ 3 + ln ⁡ 1

∫ 0 4 x - 2 2 x 2 + 7 x + 3 d x = ln ⁡ 7 - 2 ln ⁡ 3

Resolvida nossa integral!

Resposta

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x