Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Frações Parciais

Ver Teoria
Exercício 371234567891011121314151617181920212223242526272829303132333435363839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

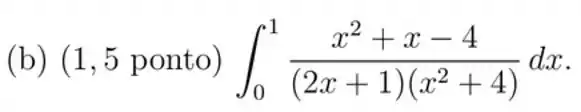
Passo 1

Vamos pegar esse termo que a gente quer integrar e abrir por frações parciais:

x 2 + x - 4 2 x + 1 x 2 + 4 = A 2 x + 1 + B x + C x 2 + 4

= A x 2 + 4 2 x + 1 x 2 + 4 + B x + C 2 x + 1 2 x + 1 x 2 + 4 = A x 2 + 4 A + 2 B x 2 + B x + 2 C x + C 2 x + 1 x 2 + 4

= A + 2 B x 2 + B + 2 C x + 4 A + C 2 x + 1 x 2 + 4

Igualando esse termo com o que queremos integrar, teremos um sistema gerado pela igualdade de cada potência de x :

A + 2 B x 2 + B + 2 C x + 4 A + C 2 x + 1 x 2 + 4 = x 2 + x - 4 2 x + 1 x 2 + 4

A + 2 B = 1 B + 2 C = 1 4 A + C = - 4

Resolvendo isso, a gente vai achar o seguinte:

A = - 1       ;       B = 1       ;       C = 0

Passo 2

Voltando à integral, teremos:

∫ x 2 + x - 4 2 x + 1 x 2 + 4 d x = ∫ - d x 2 x + 1 + x   d x x 2 + 4

A primeira integral sai por substituição:

u = 2 x + 1       ;       2 d x = d u   →     - d x = - d u 2

∫ - d x 2 x + 1 = ∫ - d u 2 u = - ln ⁡ u 2

= - ln ⁡ 2 x + 1 2

Passo 3

A segunda integral também sai por substituição:

t = x 2 + 4       ;       2 x   d x = d t   →     x   d x = d t 2

∫ x   d x x 2 + 4 = ∫ d t 2 t = ln ⁡ t 2

= ln ⁡ x 2 + 4 2

Passo 4

Assim, a integral fica,

∫ - d x 2 x + 1 + x   d x x 2 + 4 = - ln ⁡ 2 x + 1 2 + ln ⁡ x 2 + 4 2 + C

Por se tratar de um problema envolvendo uma integral definida, temos:

∫ 0 1 - d x 2 x + 1 + x   d x x 2 + 4 = - ln ⁡ 2 x + 1 2 + ln ⁡ x 2 + 4 2 0 1 =

= - ln ⁡ 2   .   1 + 1 2 + ln ⁡ 1 2 + 4 2 - - ln ⁡ 2   .   0 + 1 2 + ln ⁡ 0 2 + 4 2 =

= ln ⁡ 5 - ln ⁡ 3 + ln ⁡ 1 - ln ⁡ 4 2 = 1 2 ln ⁡ 5 12

Resposta

∫ 0 1 - d x 2 x + 1 + x   d x x 2 + 4 d x = 1 2 ln ⁡ 5 12

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x