Um bloco de de massa está pendurado na extremidade de uma corda uniforme de de comprimento e com massa igual a . Este sistema desce verticalmente mediante a aplicação de uma força de módulo igual a na extremidade livre da corda, como mostra a figura. Qual é o módulo da força exercida nos extremos da corda nos pontos A e B, respectivamente?

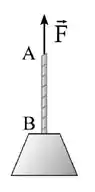
(A) e

(B) e

(C) e

(D) e

(E) e

Vamos começar com o bloco de massa .

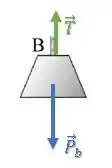
Essa força é a força de tração que o cabo está exercendo sobre o bloco.

Como temos que o bloco está descendo, vamos considerar o sentido para baixo positivo:

A força peso é dada pela massa vezes a gravidade :

Vamos fazer a mesma coisa para a corda.

Como ela é uniforme, podemos considerar que seu Centro de Gravidade está na metade da corda e aplicar a força peso nesse ponto. Porém, como estamos analisando a corda como um todo, isso não vai importar tanto.

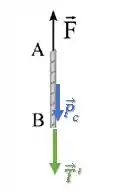
Como a corda desce junto do bloco, eles vão ter a mesma aceleração para baixo. Além disso, essa força de tração tem o mesmo valor em módulo que , ela só está representada com uma linha pois o vetor em si é diferente:

Como o módulo da tração é o mesmo, vamos simplesmente chamá-lo de :

Bom, mas quem são as trações atuando sobre os pontos A e B?

Sobre o ponto A é mole, é a própria força :

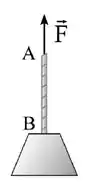
Enquanto sobre o ponto B, basta acharmos o valor de no nosso sisteminha:

Só temos duas incógnitas desconhecidas ( e ), como queremos , vamos sumir com a incógnita isolando-a na primeira equação e substituindo-a na segunda.

Primeira equação:

Substituindo isso na segunda equação, temos:

Isolando e botando em evidência o :

Agora, basta substituir os valores:

Pronto, achamos também a tração em B.

Assim, nossa resposta é: