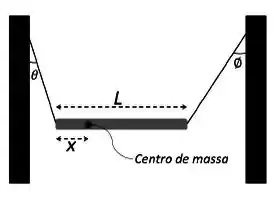
Na figura ao lado, uma barra não homogênea de comprimento L está suspensa em repouso, na horizontal, por duas cordas de massa desprezível. A corda 1 faz um ângulo com a vertical e a corda 2 faz um ângulo com a vertical.
(a) (1,5) Qual a razão T1/T2 entre as tensões na corda 1 e corda 2 respectivamente?
(b) (2,0) Em função de L, qual a distância x entre a extremidade esquerda da barra e o centro de massa?
Passo 1
a) Dá uma olhada nessas cordas da figura. A tensão nelas é paralela às cordas. Mas o peso da barra é pra baixo, na direção vertical! Então nós temos que decompor a tensão nessas cordas em horizontal e vertical. Dá uma olhada:
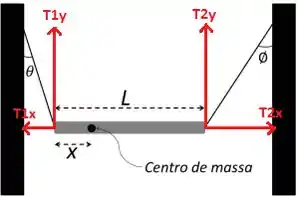
E aí vai ser:
Lembrando que também vamos ter a força peso atuando ali no centro de massa.
Passo 2
Fazendo o equilíbrio de forças:
E trocando os “valores”:
Dessa segunda relação, a gente pode tirar:
Como e :
Que a resposta do item A.
Passo 3
b) Pra achar o valor de x nós vamos usar essa informação: no equilíbrio, o somatório dos momentos vai ser zero em qualquer ponto.
Vou fazer o somatório dos momentos com relação à extremidade esquerda da barra:
Show! Guarde essa equação.
Agora, vou substituir a relação que a gente achou entre T1 e T2 nessa equação aqui:
Que é o equilíbrio de forças verticais. Então:
E como e :
Belezinha! Voltando lá naquela equação que eu pedi pra você guardar:
Vou trocar :
Arrumando a casa:
E como :
Resposta
a)
b)