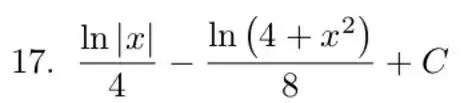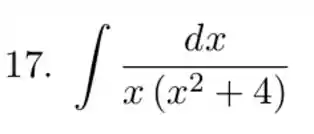
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Frações Parciais

Ver Teoria
Exercício 136123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Nesse caso aqui, temos um macete que facilita a nossa vida. Antes de começar a dividir em frações parciais, vamos fazer uma substituição na integral

u = x 2

d u = 2 x   d x  

Então

∫ d x x ( x 2 + 4 ) = ∫ d u / 2 x x ( x 2 + 4 ) = ∫ d u 2 x 2 ( x 2 + 4 ) = 1 2 ∫ d u u ( u + 4 )

Agora ficou mais simples de usar frações parciais.

Passo 2

1 u u + 4 = A u + B u + 4

Fazendo com que as frações tenham o mesmo denominador teremos

1 u ( u + 4 ) = A ( u + 4 ) u ( u + 4 ) + B u u ( u + 4 )

Se o denominador é o mesmo em ambos os lados da expressão podemos fazer

1 = A u + 4 + B u

1 = A u + 4 A + B u

1 = u A + B + 4 A

Igualando os temos de mesmo grau vamos ficar com

A + B = 0

A = 1 / 4

Então

B = - 1 / 4  

Logo

1 u u + 4 = 1 4 u - 1 4 ( u + 4 )

Passo 3

Agora vamos voltar para a integral

∫ d u u ( u + 4 ) = 1 4 ∫ 1 u d u - 1 4 ∫ 1 u + 4 d u

Sabemos que

∫ 1 u d u = ln ⁡ u

Para resolver a integral

∫ 1 u + 4 d u

Vamos utilizar a substituição

w = u + 4

d w = d u

Então ficamos com

∫ 1 u + 4 d u = ∫ 1 w d w

∫ 1 u + 4 d u = ln ⁡ w

Desfazendo a substituição

∫ 1 u + 4 d u = ln ⁡ u + 4

E substituindo na integral, ficamos com

∫ d u u ( u + 4 ) = 1 4 ∫ 1 u d u - 1 4 ∫ 1 u + 4 d u

∫ d u u ( u + 4 ) = 1 4 ln ⁡ u - 1 4 ln ⁡ u + 4

Passo 4

Tá quase pronto! Maaas, lembre que nossa variável é x . Então temos que voltar para a substituição inicial

u = x 2

d u = 2 x   d x  

Então

∫ d x x ( x 2 + 4 ) = 1 2 ∫ d u u ( u + 4 )

∫ d x x x 2 + 4 = 1 2 1 4 ln ⁡ x 2 - 1 4 ln ⁡ x 2 + 4

∫ d x x x 2 + 4 = 1 8 ln ⁡ x 2 - 1 8 ln ⁡ x 2 + 4

∫ d x x x 2 + 4 = 2 8 ln ⁡ x - 1 8 ln ⁡ x 2 + 4

∫ d x x x 2 + 4 = 1 4 ln ⁡ x - 1 8 ln ⁡ x 2 + 4 + C

Não podemos esquecer a constante de integração! Resolvido!

Resposta

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x