UnB; Cálculo 1; Lista Semana 17; “Reviso - Frações Parciais; Comprimento de arco e área”; Exercício 18f
18) Calcule as integrais seguintes:
(f)
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!
Vamos lá, pessoal! Esse é um exercício clássico de Integral por Frações Parciais. Sabemos que é uma Integral desse tipo porque a integral dessa função não pode ser calculada nem diretamente, nem por substituição de variável e nem por partes. Neste caso, devemos decompor o integrando em uma soma de frações, e então, integraremos membro a membro.
E essa função do item (f) tem uma característica muito especial. Perceba que o numerador da função tem o mesmo grau do denominador (terceiro grau).
Quando nos deparamos com isso, é interessante realizarmos a divisão entre os polinômios para tentarmos simplificar a função de alguma forma.
Então vamos nessa?
A divisão é montada da mesma forma que uma divisão entre números, veja:
Como não temos alguns graus, completaremos com :
O primeiro quociente será
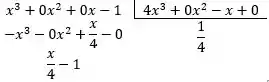
Como após a divisão o resto ficou em um grau menor que o dividendo, pararemos por aqui.
Nossa função, após a divisão, é:
Legal! O numerador está com grau menor em relação ao denominador.
Vamos retornar para a integração:
Como está em uma soma, podemos dividir essa integral:
A integral com é bem simples e, por isso, vamos deixar ela para o final. Precisamos dar uma atenção extra para :
Vamos começar aplicando MMC no numerador:
Retornando para a integral, retiraremos o que é constante em relação à :
Outra simplificação que podemos fazer é no denominador, veja:
Ah, você já reparou né? é um produto notável de .
Portanto:
Como já nos fala a regra das frações parciais, para cada fator presente no denominador original, criaremos uma fração utilizando o fator como denominador, e um valor desconhecido como numerador (normalmente chamamos de ).
Ótimo! Então, qual é a cara que a nossa função terá? Será algo do tipo:
Passo 2
O que precisamos, a partir de agora, é definir , e .
Relembrando, nossa função (após a divisão de polinômios e retirar por ser constante) começou assim:
Agora já temos:
Como precisamos encontrar , e , vamos multiplicar o denominador da função original em todos os termos dessa igualdade. Dessa forma, o lado esquerdo da igualdade será apenas e poderemos evoluir com as letrinhas:
Como já era esperado, no lado esquerdo da igualdade podemos cortar o denominador. Já no lado direito, cada um dos denominadores será cortado por um dos termos, ficando algo desse tipo:
Bacana, ficou como esperávamos né?
Uma coisa que fica claro é que podemos aplicar distributiva para multiplicar as letras pelos parênteses no lado direito da equação:
Perceba que temos outra distributiva ainda, que é a multiplicação entre os parênteses:
Para deixar mais organizado, vamos deixar os termos quadráticos no começo, os de 1º grau na sequência e os termos sem por último:
Claro que essa organização não é à toa!
Portanto, vamos juntar o termo independente do lado esquerdo da equação com o termo independente do lado direito:
Ótimo, encontramos !
Da mesma forma acontecerá para o número que acompanha a variável de 1º grau:
E como não poderia ser diferente, para os fatores de segundo grau:
Como conhecemos e , vamos substituir:
Agora só precisamos encontrar :
Passo 3
Olha só! Conseguimos finalmente transformar a nossa função original em uma função com frações parciais:
Calma, agora partiremos para a integral de fato!
Como há subtrações entre as frações, podemos dividir essa integral:
A partir de agora, olharemos para as integrais de maneira individual:
Essa integral pode ser facilmente resolvida pela tabela de substituição direta.
Ficando:
Próxima integral:
Essa integral, resolveremos por substituição:
Se ,
Ficando:
Retornando para as variáveis iniciais:
Última integral:
Da mesma forma, resolveremos por substituição:
Se ,
Ficando:
Retornando:
Passo 4
Por fim, vamos juntar tudo. Ah, não podemos esquecer que deixamos alguns caras para depois!
Vamos calcular?
é constante em relação à , portanto:
Essa integral é uma substituição direta, certo?
Então:
Agora, vamos trazer o restante da integral (não se esqueça da Constante de Integração):
Podemos encontrar o MMC dos termos dentro dos parênteses:
Como temos constante nos parênteses, podemos retirar:
Ufa! Terminamos!
Pra essa questão é isso pessoal! Bora pra mais uma?