Calcule a integral
transformando-a para um sistema de coordenadas conveniente.
Passo 1
Vamos retirar da integral as informações que a gente tem sobre o domínio, para entender quem ele é e depois descreve-lo em outras coordenadas.
Daí a gente tira que
Temos que essas duas integrais de fora descrevem uma região no plano . Vamos entender que região é essa. Vimos que
Repara que isso é o mesmo que dizer que está entre as metades da circunferência: . Ela tem raio e centro na origem.
E como . Podemos desenhar essa região assim:
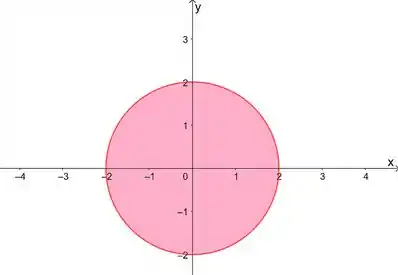
Como o nosso domínio tem forma de círculo no plano , e está definido bem entre duas funções, a gente pode usar as coordenadas cilindricas e fazer as mudanças:
Então para escrever os extremos de integração, limitamos essas variáveis que a gente tem: e . Bora lá!
Passo 2
Vamos chamar nosso domínio de . Queremos calcular
Sendo que o eixo está assim:
Ao aplicar as nossas transformações aí, ficamos com
Limitamos o ! Vamos seguir!
Passo 3
E e ? Definir elas é parecido com definir uma região em por coordenadas polares. A gente viu que estamos dentro da circunferência , aí podemos escrever que
Substituindo nossas transformações nessa inequação:
E como não há mais restrições, podemos assumir:
Belezinha?
Obs: a gente também podia limitar essas variáveis desse passo olhando o esboço da região em . Aí fica mais a seu critério mesmo.
Passo 4
Agora é montar a integral. Primeiro a gente substitui nossa transformação no nosso integrando:
Depois a gente multiplica ele por
Aí a gente pode colocar nossos extremos de integração:
Passo 5
Bora calcular essa belezura: