Seja a região do espaço definida pelas desigualdades:
(c) Escreva
Como uma integral repetida (iterada), sem contudo efetuar os cálculos, usando coordenadas esféricas, e calcule o valor da integral.
Passo 1
Para escrever a região em coordenadas esféricas é bom a gente fazer um esboço.
Vamos olhar primeiro os limites de , ele vai de até , mas quem é essa segunda equação aí?
Como os limite é apenas a raiz positiva, temos a metade superior da esfera de raio .
Olhando os limites de agora, ele vai de até
Então também se trata da raiz positiva, agora do círculo de raio no plano . O esboço fica assim
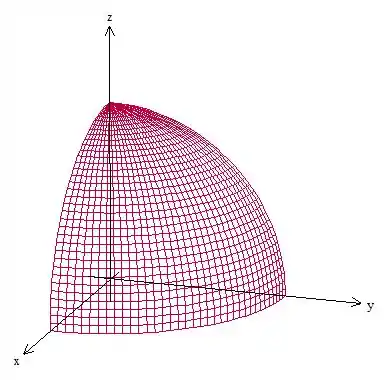
Passo 2
Em coordenadas esféricas, temos que
Passo 3
O limite do raio aqui é apenas a esfera , portanto o intervalo de integração de é
Temos dois jeitos de descobrir os limites dos ângulos e . Se olharmos para o esboço, vemos que a nossa esfera está apena no primeiro octante, certo?
Isso implica que vai apenas até , e o ângulo também vai até . Com isso
Se você não conseguiu enxergar esse ângulo isso pelo gráfico, tente treinar um pouquinho mais isso, mas existe um segundo caminho, pensa o seguinte:
Nossa esfera está limitada pelo plano , com as novas variáveis, sabemos que
Por fim, vamos substituir as novas variáveis na função dentro da integral
Passo 4
Bom, sabemos os limites, vamos montar a integral sem esquecer
Passo 5
Aqui ele pede pra resolver a integral né, vamos lá
Integrando em relação a
Vamos fazer uma substituição pra integrar isso aqui em
Voltando pra integral
Fácil de integrar agora né
Integrando em