O volume de um sólido é dado pela seguinte integral tripla em coordenadas cilíndricas:
a) Mude a integral acima para coordenadas cartesianas explicitando os limites de integração.
b) Mude a integral acima para coordenadas esféricas explicitando os limites de integração.
c) Calcule .
Passo 1
a) Vamos reunir as informações que a gente tem para tentar entender que região é essa. Ele diz que a integral está em coordenadas cilíndricas. Isso significa, que valem essas relações entre e :
E dos extremos de integração, podemos tirar essas relações:
Mas repara que a integral tripla está multiplicada por 2, o que significa que nossa região é simétrica (metades iguais), e a integral tripla apenas descreve uma de suas metades.
Como tudo isso em mente, vamos seguir. A gente consegue!
Passo 2
Vamos substituir nossas expressões da mudança de variáveis nas inequações que a gente tem para sairmos de e irmos para .
Temos
A gente viu que
Lembrando que é sempre positovo, daí a gente tira que
Substituindo na inequação:
Elevando tudo ao quadradoo
Tiramos duas inequações cartesianas daí:
Isso representa uma região abaixo de um cone para .
Porque abaixo? Repara que os valores de (nosso variável da altura ao quadrado) são menores que o resto da expressão do cone. Isso significa, que nossa região está em valores menores de do que , quando . Ou seja, abaixo de um cone.
E a temos outra inequação:
E isso é a inequação para representar a parte interior a esfera .
Passo 3
Olhando as outras inequações:
Essa diz que nossa região está dando a volta completa em relação ao eixo .
E essa diz que nossa região está entre e . Ou seja, entre e o plano que passa pela intereseção entre o cone e a esfera (para confirmar isso é só igualar as expressões de das duas equações).
Com tudo isso, vemos que a integral tripla descreve a metade de cima da região dentro da esfera e fora do cone , sem outras restrições. E o volume calculado é toda essa região. Vamos esboçar só para ter uma ideia:
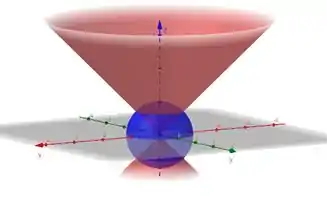
É a região dentro dessa superfície azul e fora da superfície vermelha.
Passo 4
A gente precisa montar uma integral que descreva o volume dessa região, mas em . Então precisamos achar extremos de integração para essas variáveis.
Como é um volume de uma região simétrica, a gente pode só descrever a metade superior e multiplicar a integral por .
Agora, cê concorda comigo, que o volume dessa metade da região exterior ao volume do cone é o volume da semiesfera menos o volume dessa parte em forma de pião que a gente tem ali no meio (região dentro da esfera e dentro do cone)?

Então nossa integral pode ficar:
Passo 5
Vamos montar essas integrais. Vamos limitar .
- Semiesfera
Cara, em , nossa região está entre o plano e a parte de cima da esfera . Então a gente pode escrever
E e descrevem o círculo de raio 1 . Ele é a interseção da esfera com o plano . A gente pode descrever ele em coordenadas cartesianas assim
Já que sei raio é .
Isso significa que está entre as metades da circunferência .
Passo 6
- Pião
Cara, em , nossa região está entre o cone e a parte de cima da esfera . Então a gente pode escrever
E e descrevem o círculo que é limitado pela curva de interseção entre essas duas superfícies. Vamos achar ela
A gente pode descrever ele em coordenadas cartesianas assim
Já que sei raio é .
Isso significa que está entre as metades da circunferência .
Nossa integrais ficam assim
Passo 7
b) Cara, a gente quer descrever a nossa região que está dentro da esfera e fora do cone:
Descrever essa região em coordenadas esféricas é aplicar as mudanças
E montar uma integral limitando .
Passo 8
Para fazer isso, a gente vai substituir nossas expressões para mudanças de variáveis nas equações do domínio:
Começando nessa, vamos ter:
Já que :
E a gente assume que ele começa do zero:
Passo 9
E olhando para a outra equação:
Já que . E podemos escrever
Isso porque está sempre dentro de . Então a gente escreve
Como a gente não tem mais informações, podemos assumir que dá a volta completa e as outras variáveis começam do zero:
Agora é montar a integral bonitinha. Para calcular o volume, a gente calcula uma integral tripla com argumento igual a 1. Aí aplicando a mudança de variáveis, os extremos de integração que a gente achou e multiplicando o argumento da integral pelo :
Passo 10
c) Agora é calcular essa integral que a gente acabou de montar
Prontinho!