Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 581234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule o volume do sólido

S = x , y , z   ∈   R 3 ;   z 2 ≤ 1 3 x 2 + y 2 ,     x 2 + y 2 + z 2 ≤ 4 ,   x 2 + y 2 ≥ 1  

Passo 1

Bem... se você se lembrar, um dos métodos de encontrar um volume é justamente calcular uma integral tripla, essa daqui ó

∭ S 1 d x d y d z

Onde S é justamente o nosso sólido do problema. Bora olhar pra ele com mais detalhe?!

Passo 2

Então...! O nosso sólido S está entre três superfícies bem peculiares. A primeira delas é

z 2 = 1 3 x 2 + y 2

Que nos representa, no espaço, um cone de centro na origem.

“tendi, mas não queremos isso daí. Nós queremos isso daqui z 2 ≤ 1 3 x 2 + y 2 . O que esse sinal significa?!”

Pois então... esse sinal de menor ou igual apenas está falando que se trata de um sólido na parte de fora do cone, sacou?

Analisando de modo análogo, x 2 + y 2 + z 2 ≤ 4 nos representa uma esfera de raio dois (o interior dela) e x 2 + y 2 ≥ 1 , um cilindro de raio 1 e com o eixo em z (Os pontos do lado de fora dele)

Desenhando todos juntos, podemos ver o nosso sólido S que satisfaz todas essas características de fora ou dentro. Veja só:

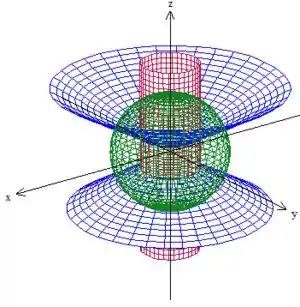
Passo 3

Como estamos falando de um sólido dentro de uma esfera, seria legal se fizéssemos uma mudança para coordenas esféricas

x = ρ sin ⁡ φ cos ⁡ θ

y = ρ sin ⁡ φ sin ⁡ θ

z = ρ cos ⁡ φ

J = ρ 2 sin ⁡ φ

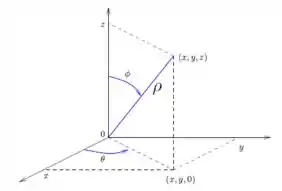
Onde o nosso ângulo θ dá uma volta completa para a nossa região, logo

0 ≤ θ ≤ 2 π

Quanto ao nosso φ , ele varia entre a parte de baixo do cone até a parte de cima, logo, para obter essa variação, vamos olhar para a equação do cone, só que agora nas novas coordenadas

z 2 = 1 3 x 2 + y 2     →     ρ cos ⁡ φ 2 = 1 3 ρ sin ⁡ φ cos ⁡ θ 2 + ρ sin ⁡ φ sin ⁡ θ 2   →

Fazendo as simplificações...

ρ 2 c o s 2 φ = 1 3 ρ 2 s i n 2 φ   c o s 2 θ + ρ 2 s i n 2 φ   s i n 2 θ → ρ 2 c o s 2 φ = ρ 2 s i n 2 φ 3 ( c o s 2 θ + s i n 2 θ ) →

c o s 2 φ = 1 3 s i n 2 φ →   s i n 2 φ c o s 2 φ = 3   →   tan ⁡ φ 2 = 3   →   tan ⁡ φ = ± 3

Portanto obteremos:

φ m i n = arctan ⁡ 3 = π 3

e

φ m á x = arctan ⁡ - 3 = 2 π 3

Lembre-se que o nosso ângulo mínimo é o π 3 pois o ângulo φ é medido de cima pra baixo como no desenho acima. ;)

Passo 4

Quanto ao nosso raio ρ ...

c i l i n d r o   v e r m e l h o ≤ ρ ≤ e s f e r a   v e r d e

Como o nosso raio está limitado inferiormente pelo cilindro, é válido agente então olhar para a sua inequação como fizemos com o cone...

x 2 + y 2 ≥ 1   →   ρ sin ⁡ φ cos ⁡ θ 2 + ρ sin ⁡ φ sin ⁡ θ 2 ≥ 1 →

De modo análogo o que fizemos anteriormente...

ρ 2 s i n 2 φ   c o s 2 θ + ρ 2 s i n 2 φ   s i n 2 θ = 1 →     ρ 2 s i n 2 φ ≥ 1 →

ρ ≥ 1 sin ⁡ φ

O raio ρ também está limitado pela esfera de raio 2 ,   logo...

1 sin ⁡ φ ≤ ρ ≤ 2

Passo 5

Montando nossa integral não se esquecendo do produto da nossa função pelo jacobiano...

V o l ( S ) = ∭ S 1 d x d y d z = ∭ S ρ , φ , θ 1   .     J   d ρ d φ d θ = ∫ 0 2 π ∫ π 3 2 π 3 ∫ 1 sin ⁡ φ 2 ρ 2 sin ⁡ φ   d ρ d φ d θ

Agora basta a gente resolver a nossa integral tripla, bora lá?! :)

∫ 0 2 π ∫ π 3 2 π 3 ∫ 1 sin ⁡ φ 2 ρ 2 sin ⁡ φ   d ρ d φ d θ = ∫ 0 2 π ∫ π 3 2 π 3 sin ⁡ φ   ρ 3 3 1 sin ⁡ φ 2 d φ d θ →

∫ 0 2 π ∫ π 3 2 π 3 sin ⁡ φ   2 3 3 - 1 sin ⁡ φ 3 3 d φ d θ →   ∫ 0 2 π ∫ π 3 2 π 3 8 3 sin ⁡ φ - 1 3 s i n 2 φ   d φ d θ →

Lembrando que 1 s i n 2 �� = c o s s e c 2 φ e d ( c o t g   φ ) d φ = - c o s s e c 2 φ , teremos

∫ 0 2 π ∫ π 3 2 π 3 8 3 sin ⁡ φ - c o s s e c 2 φ 3   d φ d θ →   ∫ 0 2 π - 8 3 cos ⁡ φ + c o t g   φ π 3 2 π 3 d θ  

Substituindo os limites de φ lembrando que c o t g   φ = cos ⁡ φ sin ⁡ φ ...

∫ 0 2 π - 8 3 cos ⁡ φ + c o t g   φ π 3 2 π 3 d θ   = ∫ 0 2 π - 8 3 cos ⁡ ( ⁡ 2 π 3 ) + cos ⁡ ( ⁡ 2 π 3 ) sin ⁡ ( ⁡ 2 π 3 ) - - 8 3 cos ⁡ ( ⁡ π 3 ) + cos ⁡ ( ⁡ π 3 ) sin ⁡ ( ⁡ π 3 ) d θ =  

Calculando esses senos e cossenos e simplificando, obteremos

∫ 0 2 π 8 3 - 2 3 3 d θ = 8 3 - 2 3 3 ∫ 0 2 π 1 d θ = 8 3 - 2 3 3 ( 2 π - 0 )

Resposta

V o l S = 2 π 8 3 - 2 3 3

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ