P3 – Cálculo Diferencial e Integral 2 – 2021.2 – Profª Cláudia Brunosi Medeiros
Calcule , onde está contida entre e no primeiro octante.
Passo 1
Vamos começar dando uma olhada em como é a essa região aí. Essa região de integração está entre aquelas duas superfícies ali que tem exatamente a equação da esfera com centro na origem:
A primeira é uma esfera com raio e a segunda é a esfera de raio . Dá uma olhada na representação dessas esferas aqui:
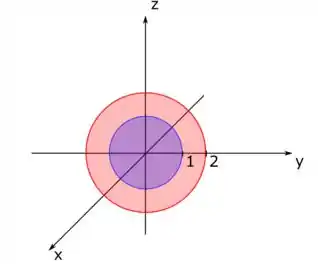
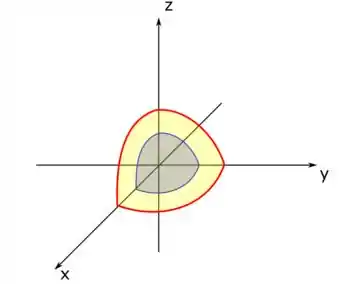
Como o problema nos fala que é a região entre essas duas esferas e que está no primeiro octante, temos que ter esse volume em amarelo aqui:
Como estamos falando de um volume associado à esferas e na nossa integral temos termos de , e vale a pena representarmos esse volume usando as coordenadas esféricas: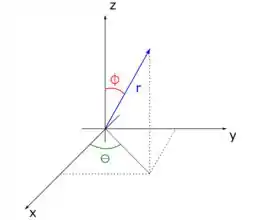
Nessas coordenadas, então, temos que o nosso volume é representado por
Passo 2
Que integral horrorosa para resolvermos hein?! Mas olha só, se usarmos as coordenadas esféricas a gente já tem que , então vamos reescrever essa integral para algo que a gente consiga resolver usando os limites da região que a gente já encontrou
Já melhorou né? Caímos em uma integral tripla iterada sob uma região retangular e a gente pode reescrevê-la como sendo o produto de três integrais:
Passo 3
Vamos começar resolvendo a integral em :
Para isso, vamos usar o método das integrais por partes escolhendo , , com isso temos
Então usamos que e temos
Para resolver essa última integral vamos ter que usar de novo o método das integrais por partes escolhendo e . Com isso a gente obtém
E escreve
Finalmente a gente tem
Passo 4
A integral em é mais direta
Passo 5
Agora podemos resolver a integral em
Passo 6
Juntando todos os nossos resultados temos que