Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 341234567891011121314151617181920212223242526272829303132333536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFMG, Sem Campus, Cálculo 3, P1 - 2021.2, Questão 4.

Calcule ∭ E z 2 d V onde E = { x , y , z : - 2 ≤ y ≤ 2 ,   - 4 - y 2 ≤ x ≤ 0 ,   0 ≤ z ≤ 4 - x 2 - y 2 . Escolha uma opção:

a) 32 π 15

b) 2 π

c) 16 π 15

d) 64 π 15

e) 3 π 2

Passo 1

Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão, a primeira coisa que temos que fazer é visualizar a região de integração de modo a descobrirmos qual é o melhor método para aplicarmos.

Já adianto que para esse caso temos uma simetria esférica, portanto temos que converter nossas coordenadas para coordenadas esféricas.

Tem alguma ideia de como fazer isso? 🤔

Para converter as coordenadas cartesianas para coordenadas esféricas, fazemos

x = ρ s e n ϕ cos ⁡ θ y = ρ s e n ϕ sen ⁡ θ z = ρ cos ⁡ ϕ x 2 + y 2 + z 2 = ρ 2 J = ρ 2 s e n ϕ

E a partir dessas conversões, podemos obter o resultado de uma maneira muito mais fácil.

Bora lá!

Passo 2

Se plotarmos a região de integração, vamos obter

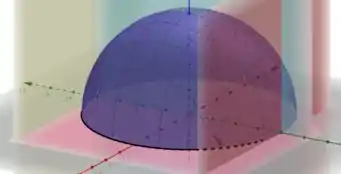
Ou seja, uma semiesfera cortada ao meio, daí, por conta dessa simetria esférica, optamos por usar esse método.

Obtendo os limites de integração, vemos que ρ varia de 0 a 2 , ϕ de 0 a π / 2 e como essa semiesfera está contida em x negativo, θ varia de π / 2 a 3 π / 2 .

Montando a nossa integral, temos

∫ π 2 3 π 2 ∫ 0 π 2 ∫ 0 2 ρ cos ⁡ ϕ 2 ρ 2 s e n ϕ d ρ d ϕ d θ

∫ π 2 3 π 2 ∫ 0 π 2 ∫ 0 2 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ d ϕ d θ

Integrando com relação a ρ ...

∫ 0 2 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = ρ 5 5 cos 2 ⁡ ϕ s e n ϕ ρ = 0 2

∫ 0 2 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = 2 5 5 cos 2 ⁡ ϕ s e n ϕ - 0 5 5 cos 2 ⁡ ϕ s e n ϕ

∫ 0 2 ρ 4 cos 2 ⁡ ϕ s e n ϕ d ρ = 32 5 cos 2 ⁡ ϕ s e n ϕ

Tranquilo até aqui? 😁

Passo 3

Integrando o resultado em relação a ϕ pelo método de substituição, fazendo u = cos ⁡ ϕ e d u = - s e n ϕ d ϕ , temos

∫ 0 π 2 32 5 cos 2 ⁡ ϕ s e n ϕ d ϕ = - 32 5 cos 3 ⁡ ϕ 3 ϕ = 0 π / 2

∫ 0 π 2 32 5 cos 2 ⁡ ϕ s e n ϕ d ϕ = - 32 5 cos 3 ⁡ π 2 3 - - 32 5 cos 3 ⁡ 0 3

∫ 0 π 2 32 5 cos 2 ⁡ ϕ s e n ϕ d ϕ = 32 15

E por fim, integrando esse resultado em função de θ ...

∫ π 2 3 π 2 32 15 d θ = 32 15 θ θ = π 2 3 π 2

∫ π 2 3 π 2 32 15 d θ = 32 15 3 π 2 - 32 15 π 2

∫ π 2 3 π 2 32 15 d θ = 32 π 15

Fim! Iae, o que achou? Responde Aí! 😁

Resposta

a) 32 π 15

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ