Determine o volume do sólido dado por
Passo 1
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.
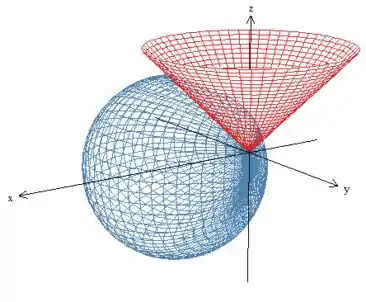
Temos uma esfera de raio centrada em e a folha superior de um cone (pois a raiz deve ser positiva).
Queremos a região que está dentro da esfera de raio (pois o enunciado pede )e, ao mesmo tempo, acima do cone (). Fazendo esses cortes, teremos então:
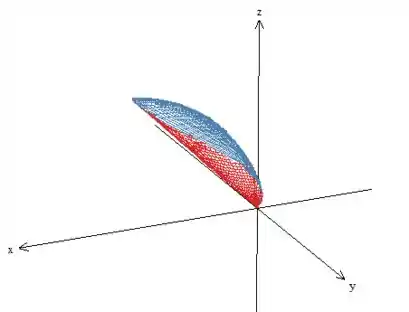
Passo 2
Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:
Passo 3
Precisamos agora escrever matematicamente a região de integração.
Os limites de são difíceis de enxergar, mas note que toda região está na parte positiva de , então podemos afirmar que , com isso . Graficamente, se projetarmos o sólido no plano fica assim:
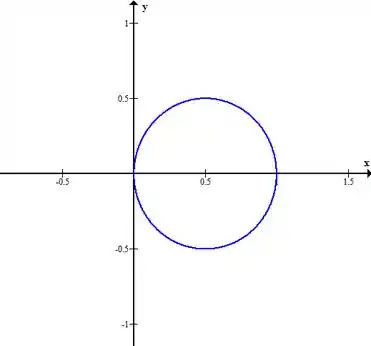
Com essa imagem também concluímos que e com isso
Os valores de , nós vemos que variam desde a origem até a superfície da esfera., vamos, então, escrevê-la em coordenadas esféricas:
Temos, então .
Falta agora o intervalo de . Pela figura, vemos que esse ângulo varia desde o eixo , onde temos até a superfície do cone. Vamos, então, escrever a equação desse cone em coordenadas esféricas:
Portanto, . A região será escrita como:
Passo 4
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 5
Agora integraremos em relação a :
Passo 6
Vamos rearrumar a integral dessa forma:
E fazer a substituição , :
Passo 7
Para resolver essa integral, vamos usar a fórmula do arco duplo :
Usando a fórmula novamente, temos