Considere o sólido que está dentro da esfera , acima do plano e abaixo do cone . Calcule o volume de utilizando coordenadas:
(b) Esféricas.
Passo 1
Caraca, que região é essa?
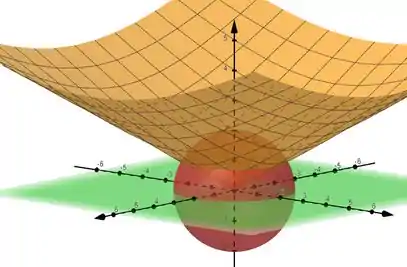
Passo 2
Primeiro passo tá dado! Agora é lembrar como que a gente acha o volume usando as coordenadas esféricas. Primeiro, essas são as substituições:
Passo 3
Bom, vamos lá então, analisando os intervalos temos que lembrar em que sentido variam as variáveis.
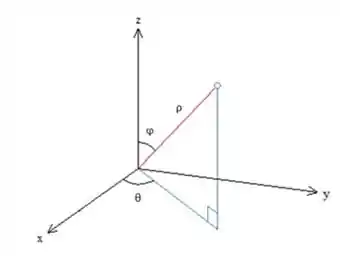
Vemos que varia simplesmente de zero a 2, nosso da uma volta completa, então varia de zero a , e o começa na parede do cone, quem tem e vai até que é.
O volume fica então
Resposta
Exercícios de Livros Relacionados
Identifique a superfície com a equação dada. ρ cos ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen θ sen ϕ