Considere a integral
(a) Reescreva como uma integral iterada em coordenadas cilíndricas.
(b) Reescreva como uma integral iterada em coordenadas esféricas.
(c) Calcule .
Passo 1
(a) Reescrevendo primeiro com coordenadas cilindricas.
Observa que a região que estamos trabalhando pode ser descrita como:
Se voce for parar pra observar primeiro o z, ficamos com:
Opa, esfera de raio 1, certo? No entano não toda ela, somente a parte acima do plano xy, até por que temos o z variando entre 0 e a parte superior da esfera.
Observando agora o y, temos:
Observa que estamos então trabalhando so com a parte positiva de y. Ou seja, só nos serve o primeiro e segundo octante.
Observando agora o x, temos que ele varia de 0 a 1. Ou seja, tambem só sua parte positiva, o que nos faz concluir que estamos trabalhando com apenas da esfera. Somente a parte contida no primeiro octante.
Passo 2
Reescrevendo então isso aí em coordenadas cilíndricas temos:
Agora vamos analizar a variação dos parametros. é relativamente simples de ver, uma vez que como estamos no primeiro ontante, ainda vai ser de 0 a 1, enquanto não vai dar a volta completa, na verdade só da volta. Variando então entre zero e .
Agora quanto a z, lembra que tinhamos:
Escrevendo entã em função da parametrização ficaremos com:
Escrevendo agora o em função da parametrização ficamos com:
Então podemos finalmente montar a integral sem esquecer o jacobiano.
Passo 3
(b) Escrevendo agora com coordenadas esféricas fica até mais tranquilo e faz mais sentido, uma vez que estamos trabalhando com um aparte de uma esfera.
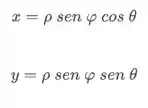
![]()
![]()
Observando a variação dos parâmetros ficamos com:
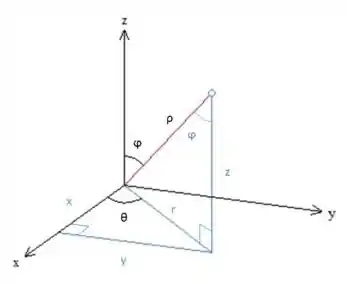
Escrevendo agora em função da parametrização ficamos com:
Montando agora a integral ficamos com:
Passo 4
(c) Para concluir agora então só nos falta calcular isso daí: