UNICAMP – Sem campus – Cálculo 2 – P2 – 5º tarde - 3
Determine o volume da região delimitada pela esfera e pelo cone
Passo 1
Fala turminha, tudo em cima? Bora lá resolver essa questão. Primeiro, vamos desenhar os dois casos. Temos o seguinte:
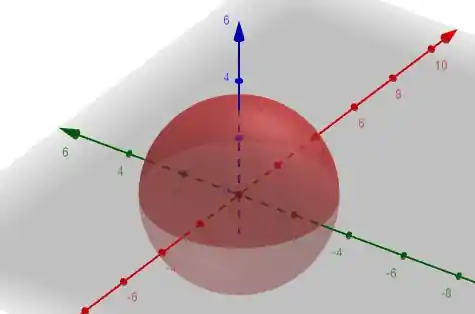
Essa nossa esfera. O cone:
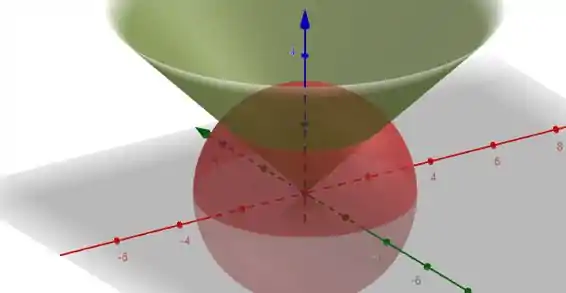
Então nosso sólido é mais ou menos um “sorvete”.
Passo 2
Vamo lá turma, precisamos que o volume que vamos formar tem formato de:
Essa integral, pode ser reinterpretada como:
Onde,
Temos que esse é a região delimitada pelas equações:
Logo, para acharmos as interseções precisamos igualar essas funções:
Resolvendo:
Passo 3
Show, agora precisamos armar a nossa integral novamente com a informação do domínio que descobrimos:
Dessa forma:
Para todo:
Utiizando coordenadas cilíndricas, vamos transformar nossa integral pra podermos resolver. Faremos aquela clássica transformação:
Para todo:
Logo, transformando nossas funções e
E o nosso domínio:
Passo 4
Nossa integral então ficou com essa cara:
Organizando essa salada mista:
Substituindo: e , temos:
Resolvendo: