Usando coordenadas esféricas, encontre o volume da região que está dentro da esfera e fora do cilindro .
Dica: Tem-se
Passo 1
Bom, se o enunciado pede volume de sólidos, sabemos que ele quer a integral tripla
Então a gente só precisa saber definir essa região em três dimensões, que já é um trabalhinho chato.
Ele fala de coordenadas esféricas no enunciado, isso quer dizer que
O esboço da região é esse aqui
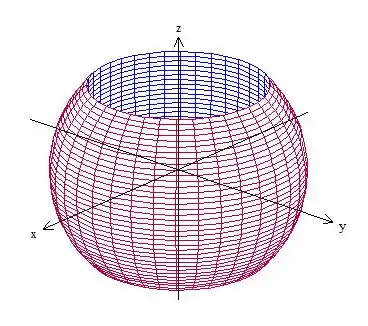
A primeira coisa que a gente pode tentar fazer é substituir isso na região do enunciado
Primeiro, ele pediu a região interna a esfera, então ele quer
Depois, ele pediu a região externa ao cilindro, logo
Colocando em evidência:
O que esse resultado quer dizer pra gente?
Ele diz que o fora do cilindro e dentro da esfera vale
Beleza, mas quais os limites de e ?
Passo 2
Pensando em primeiro, como o sólido da uma volta completa no plano , temos que os limites são
Pra ver agora podemos pensar de duas formas. A primeira – que eu pessoalmente prefiro – é olhar pros limites de .
Se isso é verdade, então podemos tirar esse e também afirmar que
Com isso
Pra isso, pensando no ciclo trigonométrico, temos que
É muito importante entender que a gente só pode fazer esse método porque o enunciado não deu nenhuma outra restrição pra ! Ele só falou do cilindro e da esfera, que já tínhamos usado em
A segunda maneira é olhar pro esboço e lembrar do significado de , que é o ângulo que começa no eixo e vai de até .
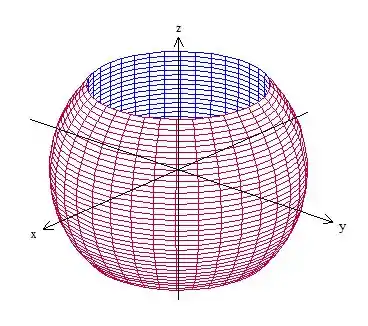
No esboço então a gente vê que o sólido começa e termina nas interseções do cilindro com a esfera, ou seja
Na equação da superfície da esfera, isso vale
E chegamos nos mesmos limites =D
Passo 3
Colocando tudo na integral tripla sem esquecer do jacobiano
Vamos começar integrando em
Isso aí a gente pode dividir em duas integrais diferentes pra organizar melhor
Passo 4
Integrando a primeira em
Integrando em
Passo 5
Vamos pra segunda integral agora
Como o enunciado deu pra gente
Então temos que
Integrando em
Passo 6
Juntando as duas integrais