Questão 1: Calcule a integral tripla:
Onde é a bola com centro na origem e raio .
Passo 1
Bem, estamos calculando uma integral tripla de soma de termos ao quadrado. Além disso, a região onde estamos trabalhando está dentro de uma esfera de raio e de centro na origem:
Logo, o problema está quase que nos implorando para resolvê-lo por uma mudança para coordenadas esféricas:
O jacobiano dessa mudança é:
E não devemos esquecer-nos da equação geral da esfera (basicamente a soma ao quadrado das coordenadas):
Passo 2
Em qualquer mudança, o problema maior é encontrar onde as novas variáveis “variam”. Mas não se preocupe, no caso das esféricas, temos um macete: comparar com variação geral das coordenadas esféricas:
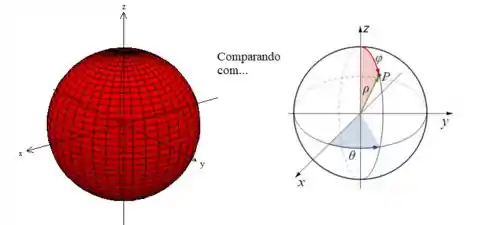
Veja que comparando a nossa região com o diagrama das variações das coordenadas esféricas, percebemos que:
- O é o cara que, no nosso caso, deve dar uma volta completa:
- O deve sair da origem e ir até o raio máximo que é dado pelo raio da bola...
- Enquanto , ele tem que sair lá de cima () e ir até lá em baixo :
Passo 3
Com essas três variações em mãos, podemos voltar a integral onde vamos substituir tudo (não se deve esquecer-se de multiplicar a função do integrando pelo Jacobiano, heim):
Integrando primeiro em ...
Integrando a do meio agora...