Calcule

Onde é o sólido limitado pela esfera de centro na origem e de raio e abaixo do cone , contido no primeiro octante.

Vamos começar esboçando essa região aí, é muito importante notar que ele só quer o sólido dentro do primeiro octante, beleza?

Ele é limitado pela esfera de raio , que é , e está abaixo do cone

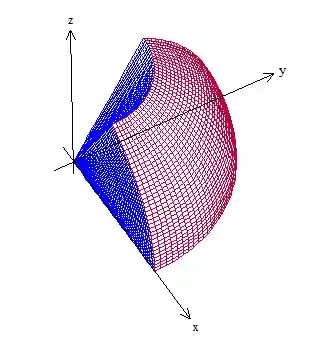
Vamos escrever isso em coordenadas esféricas, vai ajudar porque temos uma esfera de raio , temos o termo dentro da função que vamos integrar, e o cone também não fica tão ruim em coordenadas esféricas, olha só

Vamos ver como ficam as equações da esfera e do cone

Agora o cone

Perceba que o ângulo “começa” no cone e termina no plano . Isso parece meio estranho as vezes, mas o ângulo começa no eixo positivo e vai até o negativo, rodando . Ou seja, quando ele chega no plano , que é metade do caminho, ele vale .

Se você achou muito ruim essa explicação geométrica, pensa assim: o plano é

O ângulo que tem cosseno igual a é o ângulo . Beleza, então vai do cone até o plano , com isso

O ângulo é limitado apenas no primeiro octante, portanto

E o raio só é limitado pela esfera, portanto