Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 100123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 31b

Calcule ∫ ∫ ∫ R z d x d y d z , onde R é limitada por:

b) z = x - 1 2 + y 2 ; z =   - x 2 + y 2 ;   x 2 + y 2 = 4

Passo 1

Olá meu caro amigo, como está? Hoje iremos resolver uma integral tripla sobre uma região R bem interessante, veja o gráfico da querida.

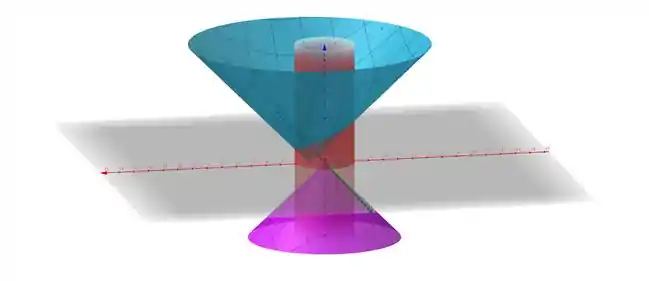
Interessante né? Não se assuste, vamos primeiro tratar de parametrizar a curva e depois seguimos.

x = r cos ⁡ θ y = r sin ⁡ θ z = z

O nosso querido jacobiano é

J = r

Passo 2

Agora vamos encontrar os intervalos para a parametrização usada

0 ≤ r ≤ 2

0 ≤ θ ≤ 2 π

x - 1 2 + y 2 → l i m i t e   s u p e r i o r   d e   z

- x 2 + y 2 → l i m i t e   i n f e r i r o   d e   z

x 2 + y 2 = 4   l i m i t e   o   p l a n o   x y

- r ≤ z ≤ r 2 - 2 r cos ⁡ θ + 1

Passo 3

Montando nossa integral

∫ ∫ ∫ R z d x d y d z

= ∫ 0 2 π ∫ 0 2 ∫ - r r 2 - 2 r cos ⁡ θ + 1 z r d z d r d θ

= ∫ 0 2 π ∫ 0 2 r 2 - 2 r cos ⁡ θ + 1 - - r 2 2 r d r d θ

= ∫ 0 2 π ∫ 0 2 - 2 r 2 cos ⁡ θ + r 2 d r d θ

= ∫ 0 2 π ( 1 4 2 2 - 1 3 2 3 cos ⁡ θ ) d θ

= 2 π

Resposta

= 2 π

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ