1) Seja o sólido dado por:
Faça os itens abaixo:
a) Faça um esboço do sólido .
b) Calcule o volume do sólido.
Passo 1
Falaaa... tudo belezinha??
Nessa questão vamos esboçar, na letra a, o sólido .
E na letra b vamos calcular o volume do sólido.
Repara que é a equação de uma esfera. Daí a gente já pensa logo em fazer mudança de variável usando coordenadas esféricas.
E pra achar o volume, calculamos a integral tripla:
Onde é o Jacobiano, que precisamos multiplicar quando fazemos mudança de variável.
Passo 2
Temos a região delimitar pela esfera e pelo cone .
Esboçando:
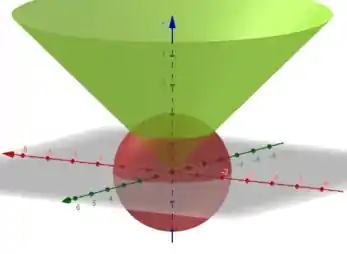
A região é limitada, na parte de baixo pelo cone e na parte de cima pela esfera.
Passo 3
Queremos, agora, achar quais são os limites de integração.
Como só a parte positiva acima do cone, então podemos isolar , na equação da esfera:
Para achar a intersecção entre a esfera e o cone, vamos igualar as duas equações:
Hum... isso é a equação de uma circunferência com raio , né?? Se a gente olhar de cima, vemos a circunferência.
Fazendo uma linha paralela ao eixo podemos destacar na figura:
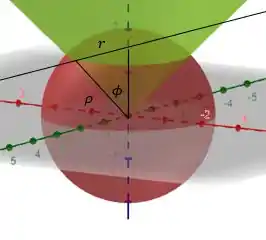
Bom... o vai variar de 0 até o raio da esfera, que é 2.
Pra achar qual é esse ângulo pode usar alguma relação trigonométrica. Como tem cateto oposto e hipotenusa:
Mas e = 2, então:
E esse seno é conhecido, né??
Daí podemos dizer que varia de 0 até .
Para o , como a volta de ta sendo completinha, então varia de 0 até .
Passo 4
Para as coordenadas esféricas, temos:
Calculando o Jacobiano:
Montando a integral tripla:
Resolvendo:
O volume do sólido é u.v.
Ufa... grandona essa, mas acabamos. Bora pra próxima?
Resposta
b)