Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1:

Determine o volume do sólido

V = x ,   y ,   z ∈ R 3 : x 2 + y 2 + z 2 ≥ 2 z ,   x 2 + y 2 + z 2 ≤ 8 z ,   x 2 + y 2 ≤ z ≤ 3 x 2 + y 2

Passo 1

Bem, um volume de um sólido V , a essa altura do campeonato, é nos dado por uma integral tripla um tanto quanto famosa:

V o l u m e   d e   V = ∭ V   1   d x d y d z

E para resolvermos essa integral dupla, antes devemos saber quem é o sólido de que estamos falando, e depois descrevê-lo. Bora?

Passo 2

Vamos começar aqui respondendo a primeira pergunta... Quem é o sólido V que estamos trabalhando?

Cara, não pira, pois esse sólido é e não é complicado ao mesmo tempo, porque precisamos apenas saber de duas superfícies basicamente, as outras duas são basicamente as mesmas saca?

Note que x 2 + y 2 + z 2 ≥ 2 z é uma esfera, mas ela está deslocada. Se levarmos para sua forma original de esfera completando quadrado...

x 2 + y 2 + z 2 ≥ 2 z         →             x 2 + y 2 + z 2 - 2 z ≥ 0       →

x 2 + y 2 + z - 1 2 - 1 ≥ 0         →

x 2 + y 2 + z - 1 2 ≥ 1

Viu só? Uma esfera de raio 1 e com o centro deslocada em z :

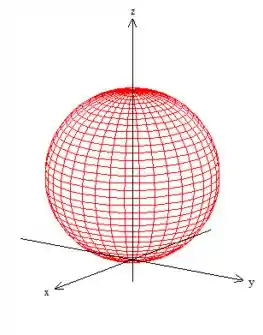
x 2 + y 2 + z 2 ≤ 8 z também é uma esfera, mas...

x 2 + y 2 + z 2 ≤ 8 z         →         x 2 + y 2 + z - 4 2 ≥ 16    

de raio 4 e centrada 4 unidades pra cima.

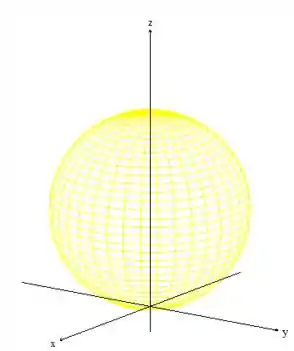
z ≥ x 2 + y 2 é um cone que delimita em baixo (representado em verde), z ≤ 3 x 2 + y 2 , um cone que delimita em cima:

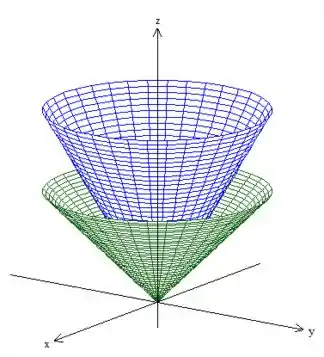
Eis o sólido V !:)

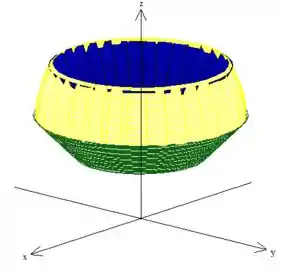
Para facilitar a nossa vida, como o sólido é simétrico em relação ao eixo z , vamos fazer uma abstração matemática:

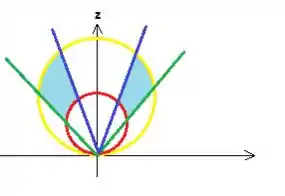
Passo 3

Bem, estamos trabalhando dentro de uma esfera, então... Nada mais justo utilizarmos as coordenadas esféricas, onde

x = r sin ⁡ φ cos ⁡ θ

y = r sin ⁡ φ sin ⁡ θ

z = r cos ⁡ φ                    

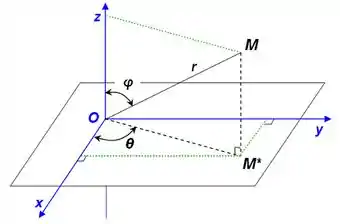
O jacobiano dessa mudança é

J = r 2 sin ⁡ φ              

Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?

Passo 4

Vamos começar aqui pelo mais fácil! Pelo ângulo θ , afinal de contas esse ângulo está dando uma volta completa, então logo ele só pode estar girando de 0 até 2 π .

0 ≤ θ ≤ 2 π

Em relação ao ângulo φ , pow, repare que ele está variando do cone superior, z = 3 x 2 + y 2 , ao cone inferior

C o n e   V e r d e ≤ φ ≤ C o n e   a z u l

Substituindo as coordenada polares nas equação dos cones... vamos ver no que dá (Veja em relação z = 3 x 2 + y 2 )

z = 3 x 2 + y 2               →               r cos ⁡ φ = 3 r sin ⁡ φ cos ⁡ θ 2 + r sin ⁡ φ cos ⁡ θ 2           →  

r cos ⁡ φ = 3 r 2 sin 2 ⁡ φ ( cos 2 ⁡ θ + sin 2 ⁡ θ )           →          

r cos ⁡ φ = 3   r sin ⁡ φ       →

Passando esse r cos ⁡ φ pro lado de lá e esse 3 pro lado de cá...

r sin ⁡ φ r cos ⁡ φ = 1 3           →         tan ⁡ φ = 1 3       →           φ = 30 ° = π 6

Sacou?

Em relação ao outro cone, z = x 2 + y 2

z = x 2 + y 2             →           r cos ⁡ φ =   r sin ⁡ φ           →                 tan ⁡ φ = 1               →

      φ = 45 ° = π 4

logo

π 6 ≤ φ ≤ π 4

Passo 5

Só nos falta o r , e pow, note que o r , entra na esfera menor, e sai na esfera maior

E s f e r a   m e n o r ≤ r ≤ E s f e r a   m a i o r

A esfera menor tem x 2 + y 2 + z 2 ≥ 2 z como equação. De modo análogo ao passo anterior, substituímos as polares para ver no que vai dar. Veja:

x 2 + y 2 + z 2 ≥ 2 z           →                 r 2 ≥ 2   r cos ⁡ φ             →

r ≥ 2 cos ⁡ φ

Enquanto que a esfera maior...

x 2 + y 2 + z 2 ≥ 8 z             →                   r 2 ≥ 8   r cos ⁡ φ       →

r ≥ 8   cos ⁡ φ

logo

2   cos ⁡ φ ≤ r ≤ 8   cos ⁡ φ

Passo 6

Com estas três variações:

2   cos ⁡ φ ≤ r ≤ 8   cos ⁡ φ

π 6 ≤ φ ≤ π 4

0 ≤ θ ≤ 2 π

Podemos retornar a integral que estamos calculando e, sem esquecer-se do Jacobiano, substituir...

V o l u m e   d e   V = ∭ V   1   d x d y d z =

∫ 0 2 π ∫ π 6 π 4 ∫ 2 cos ⁡ φ 8 cos ⁡ φ 1 ⋅ J   d r d φ d θ = ∫ 0 2 π ∫ π 6 π 4 ∫ 2 cos ⁡ φ 8 cos ⁡ φ r 2 sin ⁡ φ   d r d φ d θ

Agora é só a gente calcular! ;)

Passo 7

Calculando primeiro a integral de dentro em r , portanto tomando o seno como uma constante e saindo da integral mais interna...

∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ ∫ 2 cos ⁡ φ 8 cos ⁡ φ r 2   d r d φ d θ =

∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ r 3 3 2   cos ⁡ φ 8  cos ⁡ φ d φ d θ =

∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ 8  cos ⁡ φ 3 3 - 2  cos ⁡ φ 3 3 d φ d θ =

∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ 512   cos 3 ⁡ φ 3 - 8   cos 3 ⁡ φ 3 d φ d θ = 168 ∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ cos 3 ⁡ φ d φ d θ

Fazendo uma substituição simples para essa integral de dentro do tipo...

cos ⁡ φ = t       →           d t = - sin ⁡ φ d φ         →

sin ⁡ φ d φ = - d t

Não se esqueça de mudar os limites de integração, heim!

φ = π 6       →         t = cos ⁡ π 6 = 3 2

φ = π 4       →         t = cos ⁡ π 4 = 2 2

Então...

168 ∫ 0 2 π ∫ π 6 π 4 sin ⁡ φ cos 3 ⁡ φ d φ d θ = 168 ∫ 0 2 π - ∫ 3 2 2 2 t 3 d t d θ =

168 ∫ 0 2 π - t 4 4 3 2 2 2 d θ = 168 ∫ 0 2 π - 2 2 4 4 - 3 2 4 4 d θ =

168 ∫ 0 2 π - 4 16 4 + 9 16 4 d θ =

Enfim calculando a última integral...

168 9 64 - 4 64 ∫ 0 2 π d θ = 168 5 64 ��� 2 π =

105 4 π

Resposta

105 4 π

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ