Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Esféricas

Ver Teoria
Exercício 651234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636466676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere a região espacial:

U = x ,   y ,   z ∈ R 3 ,   z ≥ x 2 + y 2       e       x 2 + y 2 + z 2 ≤ z .

Considere a integral tripla

I = ∭ U   x 2 + y 2 + z 2     d x d y d z .

  1. Determine a fronteira de U através de igualdades de desigualdades.

    2. Considere V = U ∩ x ≥ 0       e       y ≥ 0 e considere a integral tripla

    J = ∭ V   x 2 + y 2 + z 2     d x d y d z .

  2. Escreva I em coordenadas esféricas.
  3. Escreva J em coordenadas cilíndricas.
  4. Calcule I .
  5. Sabendo que I = λ J , calcule λ .

Passo 1

Letra a) Pow, vamos, antes de qualquer coisa, entender melhor quem é a região U , beleza?

Essa região U é formada por uma inequação muito conhecida nossa: z ≥ x 2 + y 2 .

“Conhecida? eu não tô vendo ninguém conhecido aí”

Calllma! Olha só, troca esse sinal de maior apenas por um igual, assim:

z = x 2 + y 2   →

z 2 = x 2 + y 2

Epa! Viu só? Essa equação representa um cone, lembra?

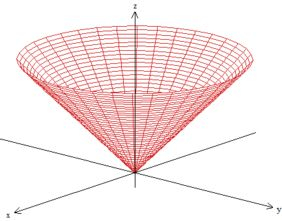
Esse sinal de maior na inequação dele ( z ≥ x 2 + y 2 ) apenas nos indica que esmos querendo um pedaço dentro dele, saca?

Pois bem, outra superfície que delimita a região é a x 2 + y 2 + z 2 = z . Essa equação têm muito uma cara de uma esfera, neh? Vamos ver então se isso é verdade

x 2 + y 2 + z 2 = z             →                       x 2 + y 2 + z 2 - z = 0

Completando quadrado em z , ou seja

z - 1 2 2 = z 2 - z + 1 2 2

então se a gente somar 1 2 2 dos dois lados da equação que estamos analisando

x 2 + y 2 + z 2 - z = 0                     →                   x 2 + y 2 + z 2 - z + 1 2 2 = 1 2 2               →

x 2 + y 2 + z - 1 2 2 = 1 2 2

Então sim! É uma esfera de raio 1 / 2 e deslocada 1 / 2 unidade pra cima em z , pegou?

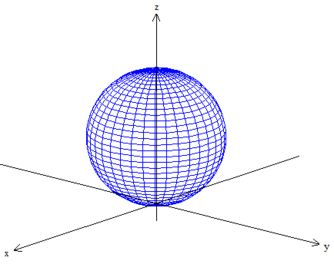
O sinal de menor em   x 2 + y 2 + z 2 ≤ z , significa que queremos a parte de dentro da esfera.

Juntando as duas superfícies

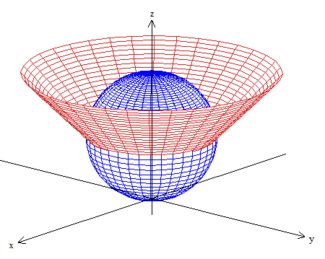
a gente nota que a região que a gente quer é

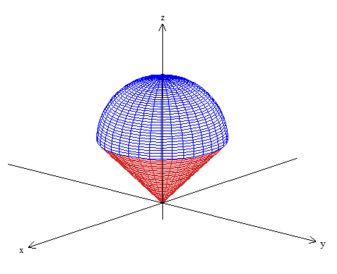
esse sorvete aí, sacou?:)

Passo 2

Pow, podemos ver no desenho da região U acima (sorvete ) que a fronteira de U é a esfera de equação

x 2 + y 2 + z 2 = z  

e também um pedacinho do cone

z = x 2 + y 2

Já temos as igualdades então. Só falta a gente saber quando é que começa quem aí! E daí que a gente vai tirar a desigualdade que o problema nos pede!

Passo 3

Cara, pelo desenho de U , a gente também pode perceber que a intersecção dessas duas superfícies é quem nos diz quem está terminando e quem está começando. Então vamos ver a intersecção dessas duas coisas nas continhas

Fazer isso, é igualar aquelas duas coisas ali

z = x 2 + y 2 x 2 + y 2 + z 2 = z               →

substituindo...

x 2 + y 2 + x 2 + y 2 2 = x 2 + y 2         →

x 2 + y 2 + x 2 + y 2 = x 2 + y 2     →

2 x 2 + y 2 = x 2 + y 2

Pow! se a gente lembrar que x 2 + y 2 representa cilindro de raio r

x 2 + y 2 = r 2

então trocando...

2 x 2 + y 2 = x 2 + y 2       →         2 r 2 = r     →

cortando um r aí...

2 r = 1     →    

r =   1 2

Pow, se o raio r = 1 / 2 , então x 2 + y 2 = 1 2 2 e pela equação do cone

z = x 2 + y 2         →                 z = 1 2 2

então

z = 1 2

Cara, agora pensa um pouco comigo, esse abaixo de z = 1 2 , que superfície a gente tem?

Exatamente! O cone ,

z = x 2 + y 2

z ≤ 1 2

e para cima desse valor, temos a esfera

x 2 + y 2 + z 2 = z

z ≥ 1 2

Beleza?

Passo 4

Letra b) Então, escrever a integral I em coordenadas esféricas é fazer a seguinte troca

x = R sin ⁡ ϕ cos ⁡ θ

y = R sin ⁡ ϕ sin ⁡ θ

z = R cos ⁡ ϕ

Não se esquecendo do jacobiano que acompanha toda mudança...

J = R 2 sin ⁡ ϕ

e nem da equação da esfera que pode nos ajudar muuuuito aqui

x 2 + y 2 + z 2 = R 2

Bem, mas o maior problema dessa mudança não é nem mudar as coordenadas, e sim determinar os limites dos novos caras ( R , ϕ e θ ), mas me acompanha que a gente vai descobrir juntos

Passo 5

Como θ é esse ângulo que varia no plano x y , a gente já pode falar de cara que θ varia de 0 a 2 π

0 ≤ θ ≤ 2 π

Quanto a esse ângulo ϕ (Que tá variando ali no eixo z ), podemos falar que ele sai de 0 , até e tá delimitado pelo cone vermelho, percebeu?

0 ≤ ϕ ≤ c o n e

Só que o cone tem equação

z = x 2 + y 2       →

substituindo essas variáveis pela mudança...

R cos ⁡ ϕ = R sin ⁡ ϕ cos ⁡ θ 2 + R sin ⁡ ϕ sin ⁡ θ 2       →

R cos ⁡ ϕ = R 2 sin 2 ⁡ ϕ cos 2 ⁡ θ + R 2 sin 2 ⁡ ϕ sin 2 ⁡ θ     →

colocando em evidência

R cos ⁡ ϕ = R 2 sin 2 ⁡ ϕ cos 2 ⁡ θ + sin 2 ⁡ θ                                 →

R cos ⁡ ϕ = R 2 sin 2 ⁡ ϕ                                                                                                     →

R cos ⁡ ϕ = R sin ⁡ ϕ                                                                                                                 →

cortando os R s...

cos ⁡ ϕ = sin ⁡ ϕ

Pow, lá da trigonometria, quem o seno e o cosseno iguais?

ϕ = π 4

Bele?

Passo 6

Bem, mas ainda falta à gente determinar quem é o raio R , correto?

Como o raio R , está variando lá na esfera, é legal a gente substituir na equação da esfera azulzinha...

x 2 + y 2 + z 2 ≤ z           →

R 2 ≤ R cos ⁡ ϕ     →

R ≤ cos ⁡ ϕ

O raio mínimo R m í n acontece quando o raio atinge o cone, percebe?

E isso acontece no ângulo ϕ máximo:

R m í n = cos ⁡ π 4 = 2 2

Logo...

2 2 ≤ R ≤ cos ⁡ ϕ

Passo 7

Montando então a integral mas agora na mudança de coordenadas para esféricas...

I = ∭ U   x 2 + y 2 + z 2     d x d y d z   →

Substituindo primeiro a função por R 2 , não se esquecendo do Jacobiano...

I = ∭ U   R 2 ∙ J   d V   →

I = ∭ U   R 2 ∙ R 2   sin ⁡ ϕ d V =  

∭ U   R 4   sin ⁡ ϕ d V

Substituindo os limites de integração que determinamos...

I = ∫ 0 2 π ∫ 0 π 4 ∫ 2 2 cos ⁡ ϕ R 4   sin ⁡ ϕ   d R d ϕ d θ

Passo 8

Letra c) Pow, como até aqui não precisamos de desenhar a região V , não nos preocupamos muito com isso, certo?

Mas agora a gente, pra descrever essa integral J em coordenas cilíndricas, vamos precisar, então vem comigo...

Bem, a única diferença dessa região V para a região U é que a região V está delimitada no primeiro octante, pois x ≥ 0 e y ≥ 0 , cacou?

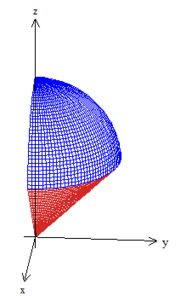
Agora vamos fazer semelhante, ao item b, mas agora vamos descrever a integral J e em coordenadas cilíndricas:

x = r sin ⁡ φ

y = r cos ⁡ φ

z = z

De forma muito parecida, a gente necessita do jacobiano, que nesse caso vale...

J = r

e é muito legal aqui a gente lembrar da equação do cilindro...

x 2 + y 2 = r 2

Bora então procurar os limites desses carinhas da mudança?

Passo 9

Bem, o primeiro deles é o ângulo φ .

Como a gente pode notar na região V desenhada acima esse ângulo que também varia no plano x y , está saindo de 0 e tá dando um quarto de volta, portanto...

0 ≤ φ ≤ π 2

Quanto ao raio r , nós já vimos que ele varia até o raio máximo que é o raio de encontro das duas superfícies, e olha que maravilha! Já determinamos esse raio no passo 3 !

0 ≤ r ≤ 1 2

Bem, quanto a variável z dessa mudança de coordenadas, bem ela...

c o n e   v e r m e l h o ≤ z ≤ e s f é r a   a z u l

como o cone tem equação,   z = x 2 + y 2

x 2 + y 2 ≤ z ≤ e s f é r a   a z u l

e a esfera, vimos que

x 2 + y 2 + z - 1 2 2 = 1 2 2   →

vamos pegar aquela equação que obtivemos no passo 1 pra facilitar as continhas pra isolar o z , certo?

Isolando o z então...

z - 1 2 2 = 1 4 - x 2 + y 2   →

z - 1 2 = 1 4 - x 2 + y 2   →

z = 1 2 + 1 4 - x 2 + y 2

Logo

x 2 + y 2 ≤ z ≤ 1 2 + 1 4 - x 2 + y 2

Pow, substituindo o x e o y pela mudança cilíndrica que fizemos...

r 2 ≤ z ≤ 1 2 + 1 4 - r 2       →

Simplificando um pouco...

r ≤ z ≤ 1 2 + 1 4 - 4 r 2 4       →

r ≤ z ≤ 1 2 + 1 2 1 - 4 r 2

Passo 10

Fazendo então a mudança de coordenas em J ...

J = ∭ V   x 2 + y 2 + z 2     d x d y d z         →

J = ∭ V   r 2 + z 2 ∙ J   d V         →

J = ∭ V   r 2 + z 2 ∙ r   d V        

Substituindo os limites que a gente acabou de determinar...

J = ∫ 0 π 2 ∫ 0 1 2 ∫ r 1 2 + 1 2 1 - 4 r 2 r 2 + z 2 ∙ r   d z d r d θ

Passo 11

Letra d) bem, como a gente já montou a integral tripla I ...

I = ∫ 0 2 π ∫ 0 π 4 ∫ 2 2 cos ⁡ ϕ R 4   sin ⁡ ϕ   d R d ϕ d θ

Basta a gente meter bronca e calcular, bora?

Começando pela integral de dentro... em R ...

I = ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ R 5 5 2 2 cos ⁡ ϕ d ϕ d θ     →

Substituindo os limites em R

I = ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ cos 5 ⁡ ϕ 5 - 2 2 5 5 d ϕ d θ     →

e dando uma arrumadinha na casa, hehe

I = ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ cos 5 ⁡ ϕ 5 - 4 2 32 ∙ 5 d ϕ d θ =

∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ cos 5 ⁡ ϕ 5 - 4 2 32 ∙ 5 sin ⁡ ϕ   d ϕ d θ

Lembrando que a integral da subtração é a subtração das integrais...

I = ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ cos 5 ⁡ ϕ 5 d ϕ d θ - ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ 2 40 d ϕ d θ

Bem, surgiu essas duas integras duplas aí, vem comigo calcular elas uma a uma!

Passo 12

Começando pela primeira

∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ cos 5 ⁡ ϕ 5 d ϕ d θ =

podemos passar essa constante pro lado de fora

1 5 ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ cos 5 ⁡ ϕ d ϕ d θ

Para resolver essa integral de dentro fazendo uma substituição simples

cos ⁡ ϕ = u           →               d u = - sin ⁡ ϕ d ϕ                   o u           sin ⁡ ϕ d ϕ = - d u

Toda mudança nos exige que encontremos os novos limites...

ϕ = 0                 →                   u = cos ⁡ 0 = 1

ϕ = π 4                 →                   u = cos ⁡ π 4 = 2 2

substituindo tudo

1 5 ∫ 0 2 π ∫ 0 π 4 cos 5 ⁡ ϕ sin ⁡ ϕ d ϕ d θ     →

1 5 ∫ 0 2 π ∫ 1 2 2 u 5 - d u d θ =

- 1 5 ∫ 0 2 π ∫ 1 2 2 u 5   d u d θ =

Note que 2 2 é menor que 1 . MAS ! se você se lembrar que podemos inverter esses limites de integração de dentro caso trocamos o sinal da integral, ficamos...

1 5 ∫ 0 2 π u 6 6 2 2 1 d θ =

1 5 ∫ 0 2 π 1 6 6 - 2 2 6 6 d θ =

simplificando tudo e integrando em θ ...

1 5 1 6 - 2 3 2 6 6 ∫ 0 2 π d θ =

1 5 1 6 6 - 1 2 3 ∙ 6   2 π 0 2 π =

1 5 1 6 - 1 48 2 π =

obteremos :)

1 5 7 48 2 π = 7 π 120

Passo 13

Resolvendo então aquela segunda integral lá do passo 11 resolvendo primeiro a integral de dentro...

∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ 2 40 d ϕ d θ =

2 40 ∫ 0 2 π   - cos ⁡ ϕ 0 π 4   d θ =

e substituindo os limites

2 40 ∫ 0 2 π   - cos ⁡ π 4 + cos ⁡ 0   d θ =

2 40 ∫ 0 2 π   - 2 2 + 1   d θ =

2 40   1 - 2 2 ∫ 0 2 π   d θ =

podemos simplificar ainda mais e...

2 40 - 2 40 ∙ 2   2 π =

2 40 - 1 40   2 π =

Obter como resultado :)

2 π 20 - π 20

E como nosso denominador antes era 120 , porque não manter? Multiplicando por 6 em cima e em baixo:

6 2 π 1 20 - 6 π 1 20

Passo 14

Pois bem! Voltando então para integral que queríamos no passo 11...

I = ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ cos 5 ⁡ ϕ 5 d ϕ d θ - ∫ 0 2 π ∫ 0 π 4 sin ⁡ ϕ 2 40 d ϕ d θ

e substituindo os velores

I = 7 π 120 - 6 2 π 120 - 6 π 120 = π 120 7 - 6 2 + 6

Ganharemos por fim (Ufa!!!! kkkkk)

= π 120 13 - 6 2

Passo 15

Letra e) Poxa! Vamos ter que calcular uma outra integral bisarra dessas?

A boa notícia é que não!

Pow, pensa um pouco: no caso de J , estamos integrando uma a mesma função em um 1 / 4 da região, correto?

Como a função é região V é simétrica em relação ao eixo z e a função x 2 + y 2 + z 2 que estamos integrando também é, quando calcularmos a integral, vamos obter

J = 1 4 I  

logo...

I = λ J       →

substituindo...

I = λ ∙ 1 4 I   →

λ = 4

Resposta

Letra a)

z = x 2 + y 2   ;           s e           z ≤ 1 2

x 2 + y 2 + z 2 = z ;                   s e                                   z ≤ 1 2

Letra b)

I = ∫ 0 2 π ∫ 0 π 4 ∫ 2 2 cos ⁡ ϕ R 4   sin ⁡ ϕ   d R d ϕ d θ

Letra c)

J = ∫ 0 π 2 ∫ 0 1 2 ∫ r 1 2 + 1 2 1 - 4 r 2 r 2 + z 2 ∙ r   d z d r d θ

Letra d)

I = π 120 13 - 6 2

Letra e)

λ = 4

Exercícios de Livros Relacionados

Identifique a superfície com a equação dada. ρ cos ⁡ ϕ = 1
Descreva em palavras a superfície com a equação dada. ρ 2 - 3 ρ + 2 = 0
Use coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas e esféricas, utiliza a que lhe parecer mais apropriada.Um cilindro sólido possui densidade constante e raio de base a e altura h .Encontre o momento de inércia do cil
Identifique a superfície cuja equação é dada. ρ = sen ⁡ θ sen ⁡ ϕ