Seja , Considere:
Considere a integral tripla
- Escreva na forma de uma integral iterada usando coordenadas esféricas e .
- Escreva na forma de uma integral iterada usando as coordenadas cilíndricas , e .
- Calcule (, .)
Passo 1
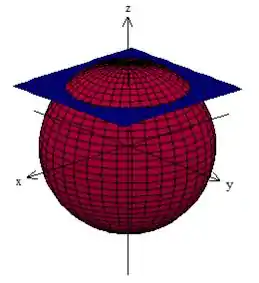
Letra a) Antes de ir partir para a mudança de coordenadas, vem comigo entender essa Região?
Se lembra dessa equação aqui: ? Ela nos representa uma esfera (menos mal, não é verdade:)?)
Logo, é uma esfera de raio e centrada na origem. Mas note uma coisinha: não estamos interessados apenas na superfície, mas no seu interior também. :D
O sólido , além de estar dentro dessa esfera, está acima do plano horizontal , dessa forma aqui
Passo 2
Agora que já sabemos quem é a superfície, podemos partir para a mudança de coordenadas esféricas. Essa daqui, veja
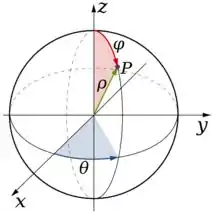
Como estamos realizando uma mudança de coordenadas, necessitaremos do Jacobiano. Se lembra? O Jacobiano da mudança para coordenadas esféricas é
Vamos agora então entendermos os limites desses novos caras.
Começando por , a gente pode observar que ele tem que dar uma volta completa para gerar o sólido, logo
Vamos agora pensar nos limites de . A gente pode observar que está entrando no sólido em baixo no plano e saindo no raio máximo da esfera
lembrando que em coordenadas esféricas, a expressão que associa é
como o plano tem equação , ganhamos
logo
Quanto a variação de , podemos notar que ele está variando de até o encontro com o plano , onde o raio assume o valor máximo . Logo devemos usar a mesma expressão de para obter o ângulo máximo, porém não esquecendo de substituir o raio máximo
Quem é o ângulo máximo entre e que dá esse valor para o cosseno? Sim, .
Passo 3
Agora podemos montar a integral: D
só dando uma arrumada nessas contas e simplificando
substituindo o Jacobiano, ganharemos por fim
ou ainda, arrumando a casa :D
Passo 4
Letra b) Lembrando das coordenadas cilíndricas, teremos
o jacobiano dessa mudança é
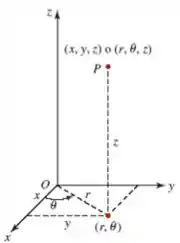
Vamos agora buscar os limites dessas variáveis.
Para os limites de e , vamos olhar para a interação da esfera com o plano
Essa equação que chagamos é a projeção do sólido no plano que é uma circunferência de raio , que é o raio máximo. Como ao raio mínimo é , temos que
enquanto isso, temos que
Sabemos que o plano tem equação , já a esfera, temos que trabalhar um pouquinho, veja
lembrando que em coordenadas cilíndricas
extraindo a raiz e lembrando que apenas queremos a parte positiva de
logo
Passo 5
Montando a integral iterada nessas coordenadas, vamos ganhar
substituindo o jacobiano
Passo 6
Letra c) Agora chegou a hora de pormos a mão na massa e resolver uma delas tendo . Note como essa segunda, em coordenadas cilíndricas, é bem mais convidativa. Bora resolver por ela?
resolvendo primeiro a integral de dentro
substituindo os limites em e simplificando
indo agora à integral do meio
por fim
Resposta
Letra a)
Letra b)
Letra c)
Exercícios de Livros Relacionados
Ver Mais
Ver Mais
Ver Mais
Ver Mais
Ver Mais