Seja o volume do sólido comum às esferas e . Expresse (sem calcular) o volume de em coordenadas esféricas na ordem .
Passo 1
Vamos, então, fazer um esboço das esferas para entender melhor o que está sendo pedido:
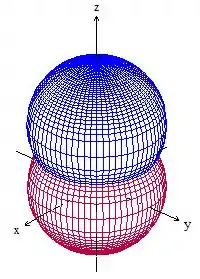
A parte que é interna às duas esferas vai ficar entre as duas calotas. Olha como fica a região
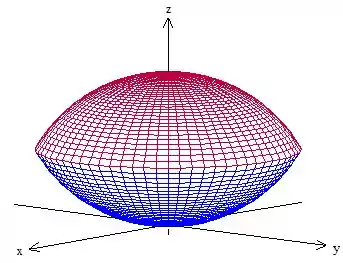
Passo 2
Vamos agora usar as coordenadas esféricas que ele pediu.
Passo 3
Precisamos escrever a região de integração.
Podemos perceber, pela figura, que , pois as esferas estão envoltas no eixo fazendo uma volta completa.
Temos um probleminha aqui. O valor de depende de qual esfera estamos pegando. Então vamos separa essa integral em duas partes. Uma parte vai ser de uma figura como se fosse uma casquinha de sorvete, nessa o vai variar de até que é o raio da esfera.
Para ver o valor de vamos ver onde as esferas se cruzam.
Vamos ter
Como fica a equação onde as esferas se cruzam.
Nesse ponto de encontro vamos ter
Substituindo os valores das coordenadas esféricas vamos ter
O valor de vai ser do eixo até esse ângulo que achamos, ou seja,
Vamos ter
Passo 4
Vamos achar a parte que falta da esfera de baixo. Os intervalos de integração vão ser iguais em pelo mesmo motivo da outra parte.
Dessa vez vai de até essa esfera, vamos substituir os valores das coordenadas esféricas para ver que valor é esse.
Então vamos ter
O valor de vai daquele ângulo que achamos ali em cima, até o plano , ou seja,
Passo 5
A integral vai ser a soma dessas duas regiões, ou seja, vai ficar assim