Considere a função . Determine:
O domínio de ;
Os interceptos;
As simetrias de ;
As assíntotas;
Intervalos de crescimento e decrescimento;
Valores máximos e mínimos locais;
Discuta concavidade e dê os pontos de inflexão;
Use a informação obtida para esboçar o gráfico de .
Passo 1
Bom, não tem nada que complique a existência da função, logo o domínio é .
Passo 2
Quando ele pede os interceptos ele deseja saber aonde esse termo cruza os eixos:
Achamos apenas um ponto, que é onde ele cruza os dois eixos de uma vez:
Passo 3
O gráfico não possui simetria, uma vez que não possui qualquer simetria.
Passo 4
Para resolver essa letra devemos levar em conta que os limites da função quando está tendendo para e para descobrir as assíntotas horizontais. Para as verticais, não teremos nenhuma, uma vez que a função é contínua ao longo de todo seu eixo :
Nesse caso aí, o vai a enquanto que ...
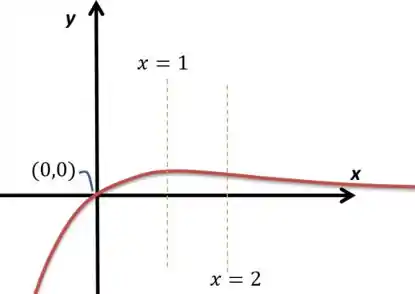
Logo, temos apenas uma assíntota, , que é horizontal.
Passo 5
Ele pede intervalos de crescimento e decrescimento. Precisamos, então, olhar para o sinal da derivada primeira:
Bom, se é sempre positivo, como toda exponencial, sabemos que o sinal só depende de . Esse termo é negativo depois de e positivo antes.
Assim, é crescente para e decrescente para .
Passo 6
Os pontos de máximo e de mínimo locais (os famosos pontos críticos) são encontrados quando ou não existe. Nesse caso, sabemos que o ponto onde isso ocorre é . Como a derivada é positiva antes e negativa depois, sabemos que ele é um ponto de máximo local, não havendo ponto de mínimo local.
Passo 7
Concavidade é derivada segunda; vamos derivar e analisar o sinal de :
Pelo resultado, notamos que o sinal só depende de . Logo, temos concavidade para baixo até e para cima daí em diante.
Passo 8
Juntando as informações:
Esboçando, fica assim.